Методы нахождения ранга

1. Метод элементарных преобразований

Ранг = числу ненулевых строк в ступенчатом виде матрицы .

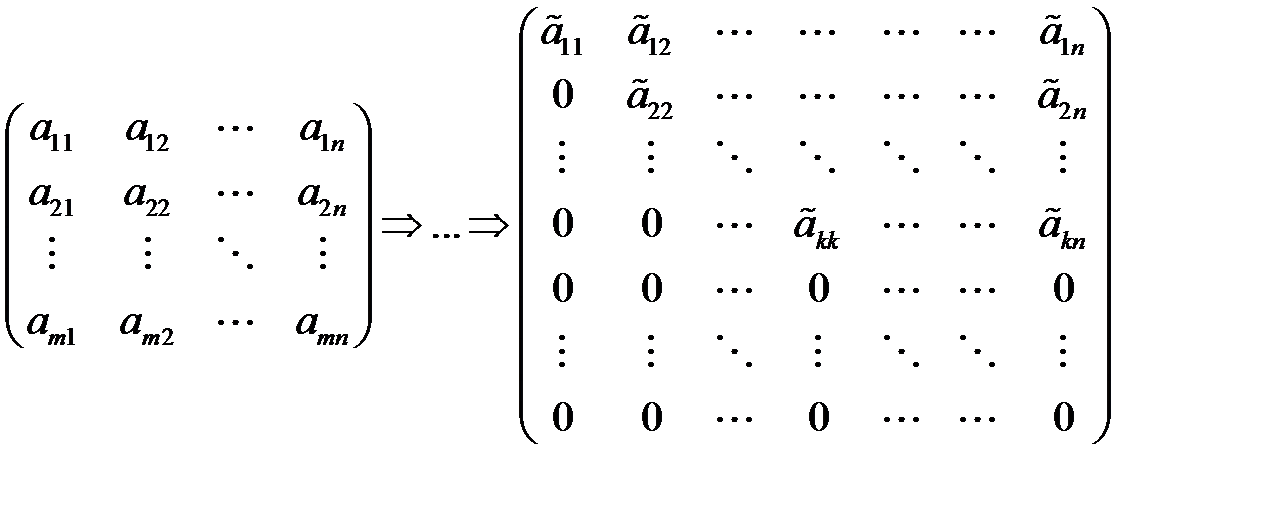
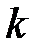ненулевых строк – ранг матрицы равен .

2. Метод миноров

Теорема о равенстве определителя нулю

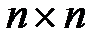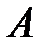Пусть - квадратная матрица . Тогда строки (столбцы) линейно зависимы.

Доказательство

Элементарные преобразования 1 и 2 (перестановка строк и прибавление к строке другой, умноженной на число) могут изменить только знак 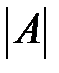. Поэтому 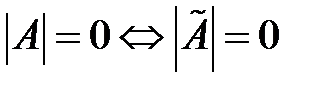, где - матрица , приведенная к ступенчатому виду. Значит имеет треугольный вид.

Получили, что определитель матрицы, имеющей треугольный вид, равен произведению элементов на диагонали. Если имеет ступенчатый, но не треугольный вид (т.е. на диагонали встречаются нулевые элементы), то , а значит имеет нулевую строку. Таким образом, 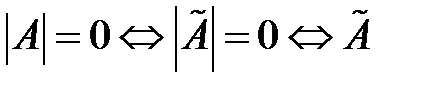имеет ступенчатый, но не треугольный вид число линейно независимых строк в .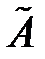

Определение

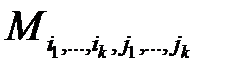Пусть . Минор порядка () – определитель, элементы которого стоят на пересечении строк 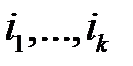и столбцов матрицы .

Теорема о ранге матрицы

Если в матрице минор порядка 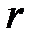, не равный 0 (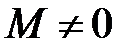), а все миноры порядка равны 0, то 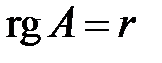. То есть = наибольшему порядку минора в 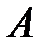, который не равен 0.

Доказательство на примере

В минор 3-го порядка , а все миноры порядка равны 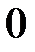(т.к. имеют 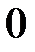-ю строчку).

[_]

Дата добавления: 2015-04-24