Квантово-механический осциллятор

Туннельный эффект. Коэффициент прозрачности барьера

Туннельный эффект - преодоление микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. Туннельный эффект — явление исключительно квантовой природы, невозможное в классической механике; аналогом туннельного эффекта в волновой оптике может служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда, с точки зрения геометрической оптики, происходит полное внутреннее отражение.

Коэффициент прозрачности барьера D: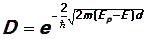

Коэффициент прозрачности характеризует вероятность прохождения частицы сквозь барьер. Эта вероятность очень сильно зависит от толщины барьера d: чем толще барьер, тем меньше вероятность туннельного эффекта.

Квантовым гармоническим осциллятором называется система, способная совершать гармонические колебания.

Гармоническим осциллятором называется система, способная совершать гармонические колебания:

h²/2m = ∆ψ + V (x, y, z) ψ = Eψ.

Это волновое уравнение описывает взаимодействие волны и корпускулы в гармоническом в квантовом гармоническом осцилляторе, который находится в стационарном состоянии и в котором энергия E механического движения существует в определенном пространстве неопределенное время в соответствии со всеобщим соотношением неопределенностей пространства и времени.

Именно поэтому в этом волновом уравнении наглядно показана зависимость потенциала V от определенных числовых значений координат определенного пространства осциллятора и не зависит от числовых значений координаты неопределенного времени. Определенная энергия E осциллятора имеет три пространственные формы своего выражения: общую, особенную и единичную.

(18/19). Модель атома Бора. Постулаты Бора. Спектр излучения атома водорода. Недостатки теории Бора. Опыт Франка – Герца

Модель Бора выявила истинное значение спектральных законов и позволила установить, как эти законы отражают квантовый характер внутренней структуры атома - устойчивость структуры атома оказалась неразрывно связанной с существованием квантов. В модели Бора каждый атом обладает некоторой последовательностью квантовых (стационарных) состояний. Каждый вид атома имеет свою последовательность квантовых значений энергии, соответствующих различным возможным стационарным состояниям.

Постулаты Бора:

1) В атоме существует ряд дискретных стационарных состояний, которым соответствуют определенные значения энергии атома E₁, E₂ и т.д. В стационарном состоянии атом не излучает и не поглощает энергии.

2) Переходя из одного стационарного состояния в другое, атом излучает и поглощает квант энергии ε = hv, равный разности энергий E_n и E_n' двух стационарных состояний: hv = E_n' - E_n.

Атом водорода (Z = 1) имеет наиболее простой линейчатый спектр излучения. Частоты спектральных линий для атома водорода и водородоподобных атомов определяются по формуле: v = R_v(1/n² – 1/n'²), где R_v = Z²me⁴/8ε₀²h³ = 3,29 · 10¹⁵ с^-1 – постоянная Ридберга.

Также эта формула может быть записана через длину волны λ: 1/λ = R_λ(1/n² – 1/n'²), где R_λ = 1,097 · 10⁷ м^-1.

Недостатки теории Бора:

- не смогла объяснить интенсивность спектральных линий.

- справедлива только для водородоподобных атомов и не работает для атомов, следующих за ним в таблице Менделеева.

- теория Бора логически противоречива: не является ни классической, ни квантовой. В системе двух уравнений, лежащих в её основе, одно - уравнение движения электрона - классическое, другое - уравнение квантования орбит - квантовое.

Опыт Франка - Герца - опыт, явившийся экспериментальным доказательством дискретности внутренней энергии атома.

В опыте наблюдался монотонный рост I при увеличении ускоряющего потенциала вплоть до 4,9 в, то есть электроны с энергией Е < 4,9 эв испытывали упругие соударения с атомами Hg и внутренняя энергия атомов не менялась. При значении V = 4,9 в (и кратных ему значениях 9,8 в, 14,7 в) появлялись резкие спады тока. Это определённым образом указывало на то, что при этих значениях V соударения электронов с атомами носят неупругий характер, т. е. энергия электронов достаточна для возбуждения атомов Hg. При кратных 4,9 эв значениях энергии электроны могут испытывать неупругие столкновения несколько раз.

Таким образом, опыт Франка - Герца показал, что спектр поглощаемой атомом энергии не непрерывен, а дискретен, минимальная порция (квант электромагнитного поля), которую может поглотить атом Hg, равна 4,9 эВ. Значение длины волны λ = 253,7 нм свечения паров Hg, возникавшее при V > 4,9 В, оказалось в соответствии со вторым постулатом Бора.

Дата добавления: 2015-04-24