Угол между прямыми на плоскости

Определение. Если заданы две прямые y = k₁x + b₁, y = k₂x + b₂, то острый угол между этими прямыми будет определяться как

.

Две прямые параллельны, если k₁ = k₂.

Две прямые перпендикулярны, если k₁ = -1/k₂.

Теорема. Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = А, В₁ = В. Если еще и С₁ = С, то прямые совпадают.

Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

10. Общее уравнение второго порядка с двумя переменными имеет вид

А х ² + В ху + С у ² + D x + Е у + F = 0, A² + В² + С² =/= 0

11. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная

Уравнение эллипса (рис.1):

Отрезок F ₁ F ₂ = 2 с, где , называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осьюэллипса. Число e = c / a, e < 1 называется эксцентриситетом эллипса.

Пусть Р (х ₁, у ₁) – точка эллипса, тогда уравнение касательной к эллипсу в данной точке имеет вид:

Условие касания прямой y = m x + k и эллипса х ² / a ² + у ² / b ² = 1:

k ² = m ² a ²+ b ².

12. Гиперболой называется геометрическое место точек, для которых разность расстояний до двух фиксированных точек плоскости, называеых фокусами, есть постоянная величина; указанная разность берется по абсолютному значению и обозначается через2а. Фокусы гиперболы обозначают буквам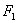и и , расстояние между ними - через 2с. По определению гиперболы , или .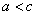

Пусть дана гипербола. Если оси декатовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение гиперболы имеет вид

(1)

где . Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат - ее центром симметрии (рис.). Оси симметрии гиперболы называются просто ее осями, центр симметрии - центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы

13. Параболой (рис.1) называется геометрическое место точек, равноудалённых от заданной точки F, называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.

Уравнение параболы (рис.1):

y ² = 2 p x.

Здесь ось ОХ является осью симметрии параболы.

Пусть Р (х ₁, у ₁) – точка параболы, тогда уравнение касательной к параболе в данной точке имеет вид:

у ₁ y = p (x + х ₁).

Условие касания прямой y = m x + k и параболы y ² = 2 p x:

2 m k = p

Дата добавления: 2015-04-24