Прямая на плоскости. Таким образом, чтобы вычислить определитель второго порядка, надо из произведения элементов главной диагонали вычесть произведение элементов побочной

2.

Таким образом, чтобы вычислить определитель второго порядка, надо из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали.

Системы двух линейных уравнений с двумя неизвестными имеют вид:

где a, b, c, d, e, f – заданные числа; x, y – неизвестные. Числа a, b, d, e – коэффициенты при неизвестных; c, f – свободные члены. Решение этой системы уравнений может быть найдено двумя основными методами

Правило Крамера. Используя определители, можно переписать формулы (3):

Формулы (4) называются правилом Крамера для системы двух линейных уравнений с двумя неизвестными.

П р и м е р. Решить систему уравнений

используя правило Крамера.

Р е ш е н и е. Здесь a = 1, b = 1, c = 12, d = 2, e = – 3, f = 14.

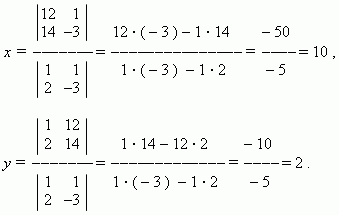
Вычисление определителей основывается на их известных свойствах, которые относятся к определителям всех порядков. Вот эти свойства:

1. Если переставить две строки (или два столбца) определителя, то определитель изменит знак.

2. Если соответствующие элементы двух столбцов (или двух строк) определителя равны или пропорциональны, то определитель равен нулю.

3. Значение определителя не изменится, если поменять местами строки и столбцы, сохранив их порядок.

4. Если все элементы какой-либо строки (или столбца) имеют общий множитель, то его можно вынести за знак определителя.

5. Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число

Определитель третьего порядка вычисляется по формуле

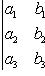
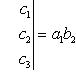
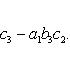(2)

Существует удобная схема для вычисления определителя третьего порядка (см. рис. 1 и рис. 2).

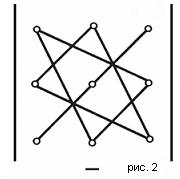
По схеме, приведенной на рис. 1, произведения соединеных элементов берутся со своим знаком, а по схеме рис. 2 - с обратным. Величина определителя равна алгебраической сумме полученных шести произведений.

3. Системы трёх линейных уравнений с тремя неизвестными имеют вид:

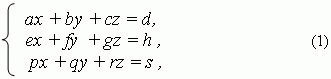
где a, b, c, d, e, f, g, h, p, q, r, s – заданные числа; x, y, z – неизвестные. Числа a, b, c, e, f, g, p, q, r – коэффициенты при неизвестных; d, h, s – свободные члены. Решение этой системы может быть найдено теми же двумя основными методами, рассмотренными выше: подстановки и сложения или вычитания.

введём понятие определителя третьего порядка. Выражение

называется определителем третьего порядка.

Метод Гаусса (метод последовательного исключения переменных)

4.

1. Сложение и вычитание матриц:

Сложение и вычитание матриц - одно из простейших действий над ними, т.к. необходимо сложить или отнять соответствующие элементы двух матриц. Главное помнить, что складывать и вычитать можно только матрицы одинаковых размеров, т.е. тех, у которых одинаковое количество строк и одинаковое количество столбцов.

Например, пусть даны две матрицы равного размера 2х3, т.е. с двумя строками и тремя столбцами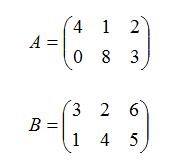

Сумма двух матриц:

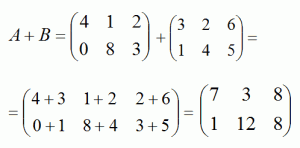
Разность двух матриц:

2. Умножение матрицы на число:

Умножение матрицы на число -процесс, заключающийся в умножении числа на каждый элемент матрицы.

Например, пусть дана матрица А:

Умножим число 3 на матрицу А:

3. Умножение двух матриц:

Умножение двух матриц возможно только при условии, что число столбцов первой матрицы должно равняться числу строк второй. Новая матрица, которая получится при умножении матриц, будет состоять из количества строк, равное количеству столбцов первой матрицы и количества столбцов, равное количеству строк второй матрицы.

Предположим есть две матрицы размерами 3х4 и 4х2, т.е. в первой матрице 3 строки и 4 столбца, а во второй матрице 4 строки и 2 столбца. Т.к. количество столбцов первой матрицы (4), равно количеству строк второй матрицы (4), то матрицы можно перемножить, новая матрица будет иметь размер: 3х2, т.е. 3 строки и 2 столбца.

Можно представить все это в виде схемы:

После того как Вы определились с размером новой матрицы, которая получится при умножении двух матриц, можно приступить к заполнению этой матрицы элементами. Если Вам надо заполнить первую строчку первого столбца этой матрицы, то надо каждый элемент первой строки первой матрицы умножать на каждый элемент первого столбца второй матрицы, если будем заполнять вторую строку первого столбца соответственно будем брать каждый элемент второй строки первой матрицы и умножать на первый столбец второй матрицы и т.д.

Посмотрим как это выглядит на схеме:

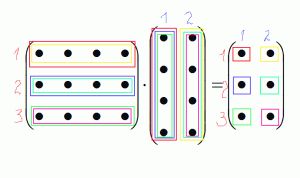
Посмотрим как это выглядит на примере:

Даны две матрицы:

Найдем произведение этих матриц:

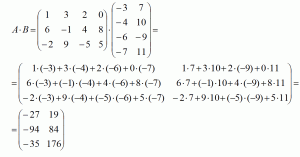
4. Деление матриц:

Деление матриц - действие над матрицами, которое в этом понятии не встретишь в учебниках. Но если есть необходимость разделить матрицу А на матрицу В, то в этом случае используют одно из свойств степеней:

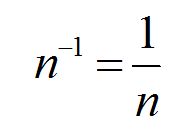
Согласно этому свойству разделим матрицу А на матрицу В:

В результате задача о делении матриц сводиться к умножению обратной матрицы матрице В на матрицу А.

Общее уравнение

Ax + By + C (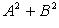 > 0).

Вектор = (А; В) - нормальный вектор прямой.

В векторном виде: + С = 0, где - радиус-вектор произвольной точки на прямой (рис. 4.11).

Частные случаи:

1) By + C = 0 - прямая параллельна оси Ox;

2) Ax + C = 0 - прямая параллельна оси Oy;

3) Ax + By = 0 - прямая проходит через начало координат;

4) y = 0 - ось Ox;

5) x = 0 - ось Oy.

Уравнение прямой в отрезках

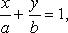
где a, b - величины отрезков, отсекаемых прямой на осях координат.

Нормальное уравнение прямой (рис. 4.11)

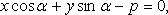
где 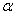- угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.

Приведение общего уравнения прямой к нормальному виду:

Здесь 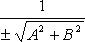- нормируемый множитель прямой; знак выбирается противоположным знаку C, если 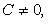и произвольно, если C = 0.

1. Уравнение прямой, проходящей через данную точку A (x ₁, y ₁) в данном направлении, определяемом угловым коэффициентом k,

y - y ₁ = k (x - x ₁). (1)

Это уравнение определяет пучок прямых, проходящих через точку A (x ₁, y ₁), которая называется центром пучка.

2. Уравнение прямой, проходящей через две точки: A (x ₁, y ₁) и B (x ₂, y ₂), записывается так:

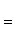
(2)

Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

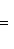
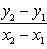
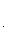(3)

3. Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B. Если две прямые заданы уравнениями с угловым коэффициентом

y = k ₁ x + B ₁,

y = k ₂ x + B ₂, (4)

то угол между ними 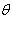определяется по формуле

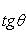
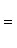
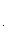(5)

4. Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k ₁ = k ₂. (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

(9)

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

(10)

Дата добавления: 2015-04-24