Векторное произведение векторов

16.

14.

15. Вектором называеься направленный отрезок(отрезок,у которого одна граничная точка считается начальной, другая - конечной).

Над буквенным обозначением вектора ставится стрелка.

Длиной вектора называеттся расстояние между началом и концом вектора.
Нулевым называется вектор,у которого начало и конец равны нулю. Его направление не определено. Два ненулевых вектора, лежащих на одной прямой или на параллельных прямых, называются коллинеарными.
Нулевой коллинеарен любому вектору.

Вектор, длина которого равна единице,называется единичным вектором.

Векторы называют равными,если они коллинеарны,имеют одинаковую длину и направление.
Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Если тройка векторов содержит нулевой вектор или пару коллинеарных векторов,то эти векторы компланарны. Векторы называют противоположными, если их длины равны,а направления противоположны.

Суммой векторов, расположенных так,что начало 1ого вектора совпадает с концом 2ого вектора, называется 3ий вектор, начало которого совпадает с началом 1ого вектора, а конец- с концом 2ого вектора.

Вектор с называется разностью векторов а и б, если с+б=а. Отсюда следует,что с = а+(-б), т.е. вычитание векторов сводится к их сложению.

Произведением вектора с на число н,называется такой вектор с, что модуль с = модуль н * а, а направление его совпадает с направление вектора а, если н>0, и ему противоположно, если число меньше 0; если а равно нулю и число = 0, то их произведение = 0.

Векторным произведением вектора 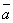на вектор 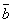называется вектор, обозначаемый символом 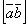и определяемый следующими тремя условиями:

1). Модуль вектора 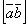равен 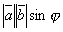, где 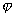- угол между векторам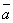и и ;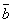

2). Вектор 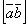перпендикулярен к каждому из вектора 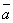и ;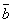

3). Направление вектора 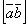соответствует «правилу правой руки». Это означает, что если векторы 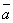, 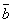и 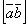приведены к общему началу, то вектор 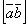должен быть направлен так, как направлен средний палец правой руки, больой палец которой направлен по первому сомножителю (то есть по вектору 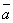), а указательный - по второму (то есть по вектору ).

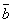Векторное произведение зависит от порядка сомножителей, именно:

.

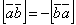Модуль векторного произведения 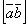равен площади S параллелограмма, построенного на векторах 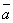и :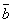

.

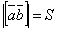Само векторное произведение может быть выражено формулой

,

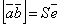где 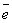- орт векторного произведения.

Векторное произведение 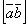обращается в нуль тогда и только тогда, когда векторы 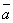и 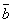коллинеарны. В частности, .

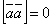Если система координатных осей правая и векторы 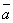и 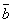заданы в этой системе своими координатами:

, ,

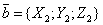то векторное произведение вектора 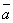на вектор 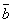определяется формулой

,

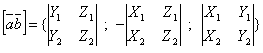или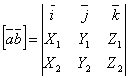

Дата добавления: 2015-04-24