Уравнение Бернулли

Выделим в стационарно текущей идеальной жидкости (физическая модель - воображаемая жидкость, в которой нет сил внутреннего трения) трубку тока, которая ограничена сечениями S ₁ и S ₂, (рис. 1). Пусть в месте сечения S ₁ скорость течения ν ₁, давление p₁ и высота, на которой это сечение расположено, h ₁. Аналогично, в месте сечения S ₂ скорость течения ν ₂, давление p₂ и высота сечения h ₂.

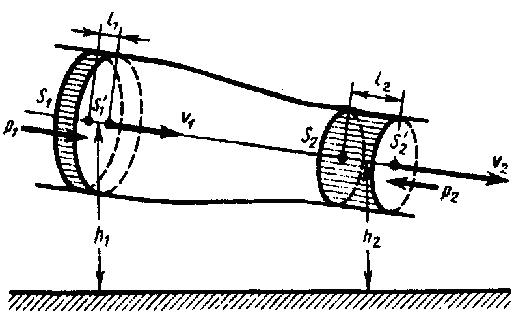
Рис.1

За бесконечно малый отрезок времени Δt жидкость двигается от сечения S ₁ к сечению S ₁', от S ₂ к S ₁'.

По закону сохранения энергии, изменение полной энергии E₂-E₁ идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы m жидкости:

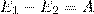(1)

где E₁ и E₂ - полные энергии жидкости массой m в местах сечений S ₁ и S ₂ соответственно.

С другой стороны, А - это работа, которая совершается при перемещении всей жидкости, расположенной между сечениями S ₁ и S ₂, за рассматриваемый малый отрезок времени Δt. Чтобы перенести массу m от S ₁ до S ₁' жидкость должна переместиться на расстояние l ₁= ν ₁Δt и от S ₂ до S ₁' - на расстояние l ₂= ν ₂Δt. Отметим, что l ₁ и l ₂ настолько малы, что всем точкам объемов, закрашенных на рис. 1, приписывают постоянные значения скорости ν, давления р и высоты h. Следовательно,

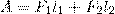(2)

где F₁ = p₁ S ₁ и F₂ = - p₂ S ₂ (отрицательна, так как направлена в сторону, противоположную течению жидкости; рис. 1).

Полные энергии E₁ и E₂ будут складываться из кинетической и потенциальной энергий массы m жидкости:

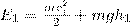(3)

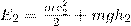(4)

Подставляя (3) и (4) в (1) и приравнивая (1) и (2), получим

(5)

Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, всегда остается постоянным, т. е.

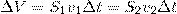
Разделив выражение (30.5) на ΔV, получим

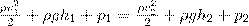
где ρ - плотность жидкости. Поскольку сечения выбирались произвольно, то

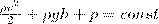(6)

Выражение (6) получено швейцарским физиком Д. Бернулли (1700-1782; опубликовано в 1738 г.) и называется уравнением Бернулли. Из его вывода видно, что уравнение Бернулли - форма закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико.

Величина р в формуле (6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела), величина ρν²/2 - динамическим давлением, величина ρgh - гидростатическое давление.

Для горизонтальной трубки тока (h ₁= h ₂) выражение (6) будет вид

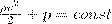(7)

где p+ρν²/2 называется полным давлением.

Из уравнения Бернулли (7) для горизонтальной трубки тока и уравнения неразрывности видно, что при течении жидкости по горизонтальной трубе, которая имеет различные сечения, скорость жидкости больше в более узких местах, а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно увидеть, установив вдоль трубы ряд манометров (рис. 2).

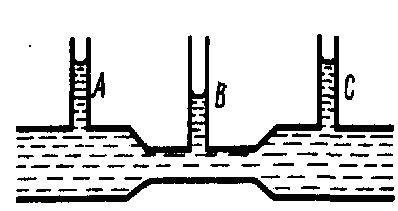
Рис.2

Данный опыт показывает, что в манометрической трубке В, которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, которые прикрепленны к широкой части трубы, что соответствует уравнению Бернулли.

Так как динамическое давление зависит от скорости движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито - Прандтля (рис. 3), состоящая из двух изогнутых под прямым углом трубок, с присоединенными к манометру противоположными концами.

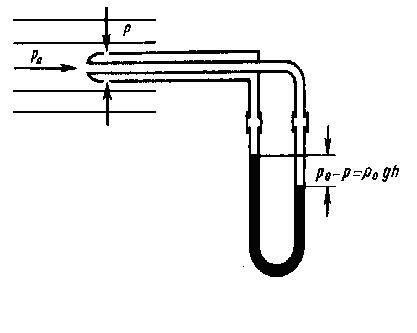
Рис.3

С помощью одной из трубок измеряется полное давление (р₀), с помощью другой - статическое (р). С помощью манометра измеряют разность давлений:

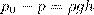(8)

где ρ₀ - плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давлению:

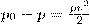(9)

Из формул (8) и (9) получаем искомую скорость потока жидкости:

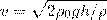
Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса (рис. 4). Струя воды подается в трубку, которая открыта в атмосферу, значит давление на выходе из трубки равно атмосферному. В трубке сделано сужение, по которому вода течет с большей скоростью. В данном месте давление меньше атмосферного. Такое же давление деалется и в откачанном сосуде, связанным с трубкой через разрыв, сделанный в ее узкой части. Воздух переносится вытекающей с большой скоростью водой из узкого конца. Таким способом можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст. =133,32 Па).

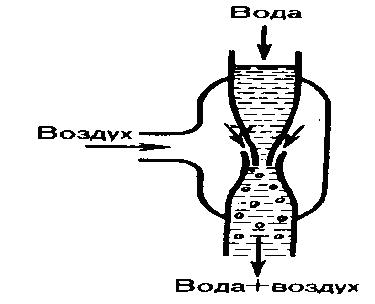
Рис.4

Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью,с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости (рис. 5).

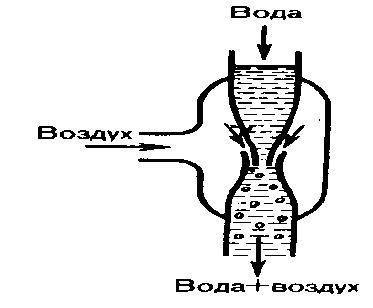
Рис.5

Рассмотрим два сечения (на уровне h ₁ свободной поверхности жидкости в сосуде и на уровне h ₁ выхода ее из отверстия) и применим уравнение Бернулли:

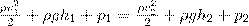
Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р₁=р₂, то уравнение будет иметь вид

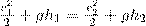
Из уравнения неразрывности мы знаем, что ν ₂/ ν ₂= S ₁/ S ₂, где S ₁ и S ₂ - площади поперечных сечений сосуда и отверстия. Если S ₁>> S ₂, то слагаемым ν ₁²/2 можно пренебречь и

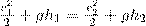
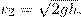
Это выражение получило название формулы Торричелли.

10) С точки зрения термодинамики под внутренней энергией тела понимают сумму кинетической энергии хаотического движения составляющих ее частиц и потенциальной энергии их взаимодействия.

Понятие теплоемкости. Дадим определение теплоемкости.

Дата добавления: 2015-04-24