
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Категоричний силогізм та його різновиди. Ентимема
|
|
|
|
Безпосередні умовиводи
Безпосередніми умовиводами називаються дедуктивні умовиводи, які виводять з одного засновку. До них належать: перетворення, обернення, протиставлення предикатові та умовивід за «логічним квадратом».
Перетворення – вид безпосереднього умовиводу, в якому змінюється якість засновків без зміни їх кількості. Перетворення будуються:
а) шляхом подвійного заперечення, яке ставиться перед зв’язкою і перед предикатом:
(S є Р → S не є не-Р),
б) заперечення переноситься з предиката до зв’язки:
(S не є Р→ S є не-Р).
Перетворенню підлягають усі 4 види суджень А, Е, І, О:
– А → Е (Всі S є Р → Жодне S не є не-Р)
– Е → А (Жодне S не є Р → Усі S є не-Р)
– І → О (Деякі S є Р → Деякі S не є не-Р)
– О → І (Деякі S не є Р → Деякі S є не-Р)
Оберненням називається такий безпосередній умовивід, в якому у висновку (новому судженні) суб’єктом стає предикат, а предикатом – суб’єкт. Обернення бувають прості (без обмежень) і з обмеженнями. Частково заперечні судження не обертаються.
Прості обернення утворюються тоді, коли і S і Р вихідного судження або розподілені, або нерозподілені.
Наприклад: «Деякі студенти – спортсмени. Деякі спортсмени – студенти».
Обернення з обмеженням можна зробити тоді, коли у вихідномусудженні суб’єкт є розподіленим, предикат – нерозподіленим, або навпаки – суб’єкт є нерозподіленим, а предикат – розподіленим.
Наприклад: «Всі свині – ссавці. Деякі ссавці – свині».
Протиставлення предикатові – такий безпосередній умовивід, у якому в новому судженні (тобто висновку) суб’єктом виступає поняття, яке суперечить предикату вихідного судження, а предикатом є суб’єкт вихідного судження, причому зв’язка змінюється на протилежну. Алгоритмом для отримання висновку для категоричного судження є:
– замість Р беремо не-Р,
– міняємо місцями S і не-Р,
– зв’язку міняємо на протилежну.
Інакше кажучи, для протиставлення предикатові треба спочатку зробити з судженням перетворення, а потім – обернення.
Наприклад: «Всі вовки – хижі тварини,
Жодна нехижа тварина не є вовком».
В абстрактному плані:
Для А – Всі S є Р → Жодне не-Р не є S;
Для Е – Жодне S не є Р → Деякі не-Р є S;
Для О – Деякі S не є Р →Деякі не-Р є S,
Для І – з частково ствердного судження необхідні висновки не робляться.
Умовиводи за «логічним квадратом» будуються на основі співвідношення А, Е, І, О, які показано в таблиці на с 33.
Категоричний силогізм – це вид дедуктивного умовиводу, в якому з двох категоричних суджень, зв’язаних середнім терміном (М), при додержанні правил обов’язково випливає висновок. У складі силогізму обов’язково повинні бути два засновки і висновок.
Поняття, що входять до складу силогізму, називають його термінами.
Більший засновок має в собі більший за обсягом термін, менший засновок – менший термін.
В основі висновку в категоричному силогізмі лежить аксіома силогізму. Все, що стверджується або заперечується стосовно виду (або члена даного класу), належить до даного роду.
Фігурами силогізму називаються форми силогізму, які розрізняються за положенням середнього терміна М у засновках. Розрізняють 4 фігури силогізму:
 Особливі правила фігур:
Особливі правила фігур:
І фігура: більший засновок повинен бути загальним, а менший – ствердним.
// фігура: більший засновок є загальним, а один із засновків і висновок – заперечними.
/// фігура: менший засновок повинен бути ствердним, а висновок – частковим.
IV фігура: загальноствердних висновків не дає; якщо більший засновок ствердний, тоді менший повинен бути загальним.
Якщо один із засновків заперечний, то більший повинен бути загальним.
Модусами категоричного силогізму називаються його різновиди, що відрізняються один від одного якісною й кількісною характеристикою засновків, що входять до нього, і висновком. Всього правильних модусів у 4 фігурах – 19.
Правила для термінів категоричного силогізму:
– в кожному силогізмі повинно бути тільки 3 терміни (S, Р, М);
– середній термін (М) повинен бути розподілений хоча б в одному із засновків;
– термін, не розподілений у засновку, не може бути розподіленим у висновку.
Правила для засновків категоричного силогізму:
– з двох заперечних засновків не можна зробити ніякого висновку;
– якщо один із засновків заперечний, то й висновок повинен бути заперечним;
– з двох часткових засновків висновку робити не можна;
– якщо один із засновків частковий, то й висновок повинен бути частковим.
Ептимемою називається скорочений категоричний силогізм, в якому пропущений один із засновків або висновок.
Наприклад: «Олександр вивчає філософію, оскільки він студент». Тут пропущений більший засновок. «Усі студенти вивчають філософію».
Відновлений з ентимеми силогізм має такий вигляд: Усі студенти вивчають філософію. Олександр – студент.
Отже, Олександр вивчає філософію.
Полісилогізмом (складним силогізмом) називаються два або кілька простих категоричних силогізмів, пов’язаних один з одним так, що висновок одного з них є засновком для іншого.
У полісилогізмі висновок попереднього силогізму стає більшим засновком наступного силогізму. Його схема:
| Приклад: | ||||
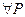 єQ єQ
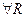 єQ єQ
| або: | Всі багатокутники – геометричні фігури. Всі трикутники – багатокутники. | ||
| Отже: | 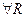 єP єP
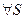 єR єR
| Отже: | Всі трикутники – геометричні фігури. Всі рівносторонні трикутники – трикутники. | |
| Отже: | 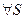 єQ єQ
| Отже: | Всі рівносторонні трикутники – геометричні фігури |
| Логічна формула епіхейреми: | 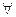 M є Р, тому що M є Р, тому що 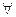 M є N M є N
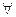 S є М, тому що S є М, тому що 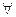 S є Q
Отже: S є Q
Отже: 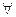 S є Р S є Р
| |
| Аналіз першого засновку: | 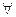 N є P N є P
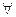 M є N M є N
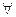 M є P M є P
| |
| Аналіз другого засновку: | 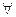 Q є M Q є M
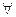 S є Q
S є M S є Q
S є M
| |
| Висновок: | 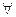 M є Р M є Р
| |
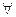 S є M, S є M,
| ||
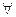 S є Р S є Р
|
|
|
|
|
|
Дата добавления: 2015-05-22; Просмотров: 823; Нарушение авторских прав?; Мы поможем в написании вашей работы!