Количество жидкости, проходящее через сечение за единицу времени,

ЗАКОН СОХРАНЕНИЯ МАССЫ

Количество вещества, проходящее через поперечное сечение потока, можно измерить в единицах массы, объёма или веса. Это количество зависит, очевидно, от скорости движения, величины сечения и времени наблюдения.

Согласно Рис.15, через сечение 1-1 за время t пройдет объём жидкости, равный объёму цилиндра 1-1-1¢-1¢, то есть V₁ =J₁×w₁×t, и масса жидкости m₁=r₁×J₁×w₁×t.

    1 1^’       Рис.15 Иллюстрация к выводу закона сохранения массы

На пути движения от начального сечения к конечному форма поперечных сечений потока может меняться самым причудливым образом, однако то массовое количество жидкости, которое прошло за время t через любое сечение, должно остаться неизменным. Это следует из закона сохранения массы. для Рис.15:

r1×J1×w1×t = r2×J2×w2×t.

(26)

Поскольку время можно выбирать произвольно, удобно сравнивать количества жидкости, проходящие за единицу времени (l с, 1 мин, 1 час и т.д.).

называется расходом.

Q =J×w	- объемный расход	(27)
Qm = r×J×w=r×Q=m/t	- массовый расход	(28)
QG = r×g×J×w=r×g×Q=G/t	- весовой расход	(29)

Для жидкости плотность r можно считать постоянной величиной. Это следует из закона Гука.

Закон Гука определяет связь между напряжением и объемной деформацией при всестороннем сжатии жидкости:

Dp = - E×e

Здесь E - модуль объёмной упругости жидкости, e = DV/V - относительное изменение объёма, V - первоначальный объем. Знак минус показывает, что при увеличении давления объём жидкости уменьшается.

Модуль упругости стали E_ст =2×10¹¹Па, а модуль упругости воды E= 2×10⁹Па. Вследствие высокого модуля упругости жидкости сжимаются незначительно. Так, при повышении давления на 10МПа, изменение объёма равно:

.

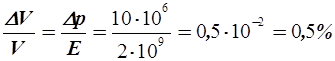Поэтому чаще всего в гидравлических расчетах жидкость считают несжимаемой и плотность жидкости r =m/ V принимается величиной постоянной и независящей от давления:

Принимая r =const, вместо (26) получим:

J1×w1 = J2×w2=.......=Q = const.

(30)

Уравнение (30) выражает закон постоянства объемного расхода по длине потока.

Дата добавления: 2015-05-23