Порядок расчета. Численный способ решения

Численный способ решения

З адача решается методом последовательных приближений- методом итераций [9]. Как известно из математики, для применения этого метода необходимо представить уравнение (54) в виде: аргумент равен функции от аргумента - Q =f(Q).

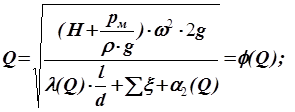(44)

· Задаемся некоторым начальным значением l_o коэффициента трения и значением коэффициента Кориолиса a_о. Если в результате анализа исходных данных можно предположить ламинарный режим (высокая вязкость жидкости), то l_o = 64/ Re_кр, и a_о =2;если турбулентный (малая вязкость и значительная шероховатость труб), то l_o =0,11×(D_э/d)^0,25 и a_о =1 (предполагается режим квадратичных сопротивлений).

· Определяется правая часть уравнения (44) - функция f(Q), то есть начальное значение расхода жидкости Q_o.

· Определяется число Re_o=4×Q_o×r/(p×d×h, уточняется режим движения и определяется значение l₁ коэффициента трения по уточненным формулам:

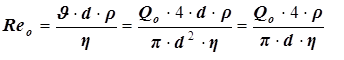
Reо < 2300	l1= 64 / Reо, a1=2.
Reо > 2300	l1 = 0,11 ×( 68 /Reо + Dэ/d)^0,25, a1=1.

· Определяется правая часть уравнения (44) - функция f(Q), то есть последующее значение расхода жидкости Q₁.

· Сравниваются расходы Q₁ и Q_о. Если они отличаются на заданную точность, расчет прекращается. Если нет, то повторяются пункты 3¸5 до тех пор, пока последующее и предыдущее значение расхода не совпадут с заданной точностью.

Принимаем для стальных умеренно заржавленных труб D_э = 0,2мм. Судя по исходным данным – жидкость маловязкая и можно предположить турбулентный режим движения.

В нашей задаче l_o =0,11×(D_э/d)^0,25 =0,11×(0,2/80 ) ^0,25=0,025; Q_o =0,0159; Re₀ =1,38×10⁵; l₁ = 0,11 ×( 68 / 1,38×10⁵ + 0,2/80 )^0,25 = 0,026; Q₁ =0,0157. Re₁ =1,36×10⁵; l₂ = 0,11 ×( 68 / 1,36×10⁵ + 0,2/80 )^0,25 = 0,026; Q₂ =0,0157

Q₁ = Q₂ = Q =0,0157м³/с - расчетное значение расхода.

В нашем примере после второго приближения расчет можно закончить.

Метод итераций - один из наиболее распространенных методов численного решения уравнений, легко реализуется на ЭВМ.

В случае ламинарного режима движения:

l= 64/ Re = 64 ×p×d×h/( 4 ×Q×r)

и уравнение (43) превращается в квадратное уравнение относительно расхода.

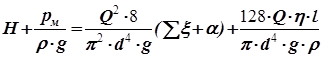
(45)

Корни уравнения (45) легко определяются.

Дата добавления: 2015-05-23