Определение диаметра трубопровода

Определение диаметра трубопровода и кавитационный расчет

По сифонному сливу (l = 50м, d =?, шероховатость трубопровода D_э =0,06мм) подается топливо (r =840кг/м³, n =5,5×10^-6м²/с) с расходом

Q = 0,01м³/с при разности отметок уровней в резервуарах H =1,38м.

На сливе имеется фильтр для светлых нефтепродуктов, два колена и вентиль, который полностью открыт.

Даны также высоты h₀ =3м и b =2м., давление насыщенных паров при температуре перекачки р_н.п. = 3кПа, р_ат =10⁵Па.

Определить диаметр трубопровода и проверить условие нормальной работы сифона.

    Рис.19 Схема к задаче

Поскольку все необходимые пояснения и теоретические основы применения уравнения Бернулли были подробно сделаны при решении задачи 1, закон сохранения энергии для данной задачи выводится без подробных пояснений. Сначала определим диаметр трубопровода.

1. Выбираем два сечения 1-1 и 2-2, а также плоскость сравнения 0-0 и записываем в общем виде уравнение Бернулли:

,

где р₁ и р₂ – абсолютные давления в центрах тяжести сечений; J₁ и J₂ – средние скорости в сечениях; z₁ и z₂ – высоты центров тяжести сечений относительно плоскости отсчета 0-0; h_1-2 –потери напора при движении жидкости от первого до второго сечения.

2. Определяем слагаемые уравнения Бернулли в данной задаче.

· Высоты центров тяжести сечений: z₁ =0; z₂ = - H;

· Средние скорости в сечениях: J₁ = Q/w₁;J₂ = Q/w₂; J_тр = Q/w.

Так как w₁ >> /w, и w₂ >> /w, то J₁ << J_тр и J₂ << J_тр; можно принять

J₁ = J₂ =0 по сравнению со скоростью движения в трубопроводе.

Другими словами, слагаемое h_1-2, которое пропорционально J_тр, много больше слагаемых a₁ × J₁ ² /2g и a₂ × J₂ ² /2g и имиможно пренебречь.

· Абсолютное давление в первом сеченииравно атмосферному,

р₁ = р_ат;

· Абсолютное давление в сечении 2-2 равно атмосферному, р₂ = р_ат.

· Потери напора h_1-2 складываются из потерь напора на трение по длине потока h_дл и потерь на местные гидравлические сопротивления å h_м

h_1-2 = h_дл + å h_м.

· Потери по длине равны

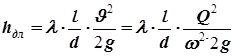. (принимаем J_тр = J).

· Местные потери напора равны:

å h_м = å x× J²/( 2 g) = å x× Q²/(w²× 2 g); где å x = x_ф + 2 x_пов + x_в + x_вых.

x_ф =1,7; x_пов = 0,23; x_в = 0,15; x_вых = 1 (Приложение 6).

å x = 1,7 + 0,46 + 0,15 +1 =3,31.

· Суммарные потери напора равны:

h_1-2 = (l×l/d+åx) × Q²/(w²× 2 g).

3. Подставляем определенные выше величины в уравнение Бернулли и решаем его относительно диаметра.

В нашей задаче закон сохранения энергии имеет вид:

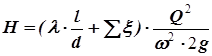. (46)

Это расчетное уравнение для определения диаметра трубопровода.. Оно представляет собой закон сохранения энергии для данной задачи. Диаметр входит в правую часть уравнения непосредственно, а также в коэффициент трения l через число Re (Re = 4Q/(p×d×n)!

Не зная диаметр, невозможно определить режим движения жидкости и выбрать формулу для l. Кроме этого, коэффициент трения зависит от диаметра сложным образом (см. формулы (37) и (38)). Если подставить эти выражения в формулу (46), то полученное уравнение не решается алгебраическими способами (является трансцендентным). Такие уравнения решаются графическим способом или численно с помощью ЭВМ (чаще всего методом деления отрезка пополам).

Дата добавления: 2015-05-23