Расчет газопроводов

При решении задач на расчет газопроводов нужно учитывать, что плотность совершенного[10] газа зависит от давления и температуры: r=p / RT

Это уравнение состояния газа (уравнение Клайперона). Здесь R – газовая постоянная, равная для воздуха 287дж/кг×°К.

В разных сечениях трубопроводной системы давление может отличаться на десятки атмосфер. Это приводит к существенному различию плотностей в сечениях газового потока и, как следствие, к различию объёмных расходов.

При движении газа в сечениях потока сохраняется массовый расход!

Q_m = r₁×J₁×w₁ = r₂×J₂×w₂ =……= r_i×J_i×w_i =const (49)

Как известно, капельная жидкость в сечении обладает потенциальной и кинетической энергией.

Газы обладают потенциальной, кинетической и внутренней энергией.

Внутренняя энергия газа зависит от температуры и вида процесса, по которому измененяется его состояние.

Если при движении газа по трубам вследствие теплообмена с окружающей средой температура по длине не изменяется, то имеет место изотермический процесс (T= const). При этом внутренняя энергия в сечениях трубопровода остается постоянной. Уравнение Бернулли при изотермическом течении газа имеет такой же вид, как и для несжимаемой жидкости, за исключением того, что в сечениях потока разная плотность:

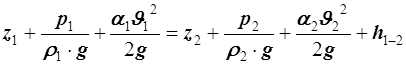. (50)

Основные задачи при расчете газопроводов

1. Определить расход газа, если известны давления в начале и конце газопровода.

2. Определить давление в сечении газопровода, если известен расход газа и давление в каком –нибудь другом сечении.

3. Определить диаметр газопровода, если известны давления в начале и конце газопровода и расход.

Для решения этих задач получим зависимость между массовым расходом газа и давлениями в сечениях 1-1 и 2-2 (Рис. 22).

4.7.1. Вывод расчетных зависимостей для совершенного газа

При движении газа в трубопроводе постоянного диаметра одновременно изменяются давление, плотность и скорость движения. Так, давление уменьшается из-за необходимости совершать работу по преодолению силы трения, плотность также уменьшается (при изотермическом течении она пропорциональна давлению). Средняя скорость движения газа увеличивается по ходу его движения, так как массовый расход остается постоянным, а плотность падает. Таким образом, использовать в явном виде уравнение Бернулли (50) для расчета нельзя.

Применим уравнение (50) к элементу газопровода длиной dl, на котором можно считать постоянными скорость и плотность газа.

Рис. 22

Схема к выводу расчетных зависимостей при движении газа

Уравнение Бернулли для выделенного элемента:

р/rg = (p+dp)/rg + dh_дл (51)

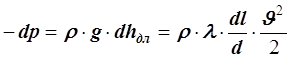
Потери на трение определяются по тем же формулам, что и для несжимаемой жидкости. Коэффициент трения l=f(Re, D_э/d).

Докажем, что при изотермическом течении, когда постоянна вязкость, по длине трубы число Re не изменяется.

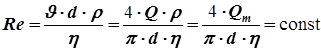
Следовательно, коэффициент трения также постоянен по длине трубопровода.

Выразим в уравнении (51) скорость и плотность через параметры в начальном сечении и массовый расход.

r×J²=r×Q_m²/ r²w² = Q_m²/ rw² = Q_m²×p₁/ r₁×p×w².

Здесь учтено, что по уравнению состояния p/ r = p₁/ r₁ = RT =const.

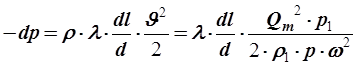
Разделяем переменные, учитываем, что w =p×d²/4, интегрируем и получаем следующие расчетные формулы:

Определение давления при известном расходе

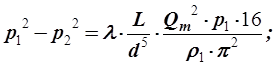(52)

Определение массового расхода при известных давлениях р₁ и р₂:

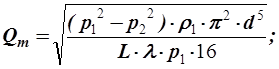(53)

Коэффициент трения определяется по тем же формулам, что и для ньютоновской жидкости:

l= 64 /Re - ламинарный режим

l= 0,11 ( 68 /Re+D_э/d)^0,25 - турбулентный режим

Так как коэффициент трения l зависит от числа Rе и, следовательно, от расхода, при определении массового расхода по формуле (53) сначала нужно задаться величиной l (например, l= 0,02), определить расход в первом приближении и затем уточнить значение l и Q_m. Как это делается, проиллюстрировано на примере расчета.

4.7.2. Пример расчета

Воздух при t=2°C движется по трубопроводу диаметром d=0,1м и длиной 15км. Давление в начале трубопровода 4,41Мпа, а в конце 0,29 Мпа. Определить массовый расход. Трубопровод изготовлен из новых стальных сварных труб.

Решение задачи.

Используем формулу (53).

Здесь неизвестны плотность газа в начале трубопровода r₁ и коэффициент трения.

· Определяем плотность газа в начале трубопровода.

r₁ = р₁/RT =4,41×10⁶/287/275=56,6кг/м³.

Здесь R =287 – газовая постоянная для воздуха, T =273+2=275 –абсолютная температура.

· Предполагаем турбулентный режим движения, задаемся величиной

l = 0,02 и вычисляем в первом приближении массовый расход:

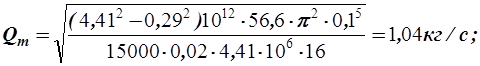
· Определяем число Re и режим движения газа.

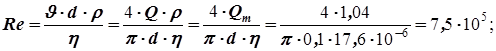
Коэффициент динамической вязкости определяем с помощью Приложения 3.

При р =98кПа и t =2°C - n =13,9×10^-6м²/с, плотность r =1,27кг/м³, следовательно:

h = n×r = 13,9×10^-6 × 1,27 = 17,6×10^-6 Па×с.

· Уточняем значение коэффициента трения. При турбулентном режиме:

l=0,11(68/Re+D_э/d)^0,25 = 0,11(68/ 7,5×10⁵ +0,1×10^-3/0,1)^0,25 = 0.0199=0,02.

Для новых стальных сварных труб D_э =0,1мм.

Таким образом, значение коэффициента трения практически не изменилось и массовый расход газа определен правильно.

Дата добавления: 2015-05-23