Расчет трубопроводов. Примеры решения задач

Большинство гидродинамических задач нефтегазовой практики связано с движением жидкости по различного рода трубопроводным системам. При этом необходимо знать количество протекающей жидкости или газа (расход) и энергетические характеристики, зависящие от давления и положения жидкости в поле силы тяжести (высот z). Часто возникает и обратная задача – при известном расходе и энергетических характеристиках определить диаметр трубопровода. Далее на конкретных примерах рассмотрены способы решения этих и некоторых других задач.

4.6.1. Определение силы или давления

Определить силу R, которую нужно приложить к поршню насоса диаметром D =65мм, чтобы подавать в бак бензин (плотность r = 765кг/м³, кинематический коэффициент вязкости n = 0,4сСт) с постоянным расходом Q = 2,5л/с. Высота подъёма жидкости в установке H₀ = 10м, показание манометра р_м0 =0,15МПа. Размеры трубопровода l =60м, d =30мм; его эквивалентная шероховатость D_э =0,03мм; коэффициент сопротивления вентиля x_в =5,5.

Рис.16

Схема к задаче

Решение

1. Выбираем два сечения 1-1 и 2-2, а также плоскость сравнения 0-0 и записываем в общем виде уравнение Бернулли:

.

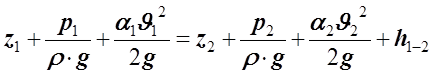Здесь р₁ и р₂ – абсолютные давления в центрах тяжести сечений; J₁ и J₂ – средние скорости в сечениях; z₁ и z₂ – высоты центров тяжести сечений относительно плоскости отсчета 0-0; h_1-2 –потери напора при движении жидкости от порвого до второго сечения.

Правила выбора сечений: · Сечения выбираются всегда перпендикулярно направлению движения жидкости и должны располагаться на прямолинейных участках потока. · Одно из расчетных сечений необходимо брать там, где нужно определить давление р, высоту z или скорость J, второе, где величины р, z, и J известны. · Нумеровать расчетные сечения следует так, чтобы жидкость двигалась от сечения 1-1 к сечению 2-2.

В нашей задаче сечение 1-1, откуда начинается движение жидкости, выбрано по поверхности поршня, так как именно в центре тяжести этого сечения необходимо определить давление жидкости. Далее, из условия равномерного движения поршня, можно определить силу R.

Сечение 2-2 выбрано по поверхности жидкости в напорном баке, так как там известны все слагаемые, составляющие удельную энергию жидкости.

Для определения величин z нужно выбрать положение плоскости сравнения (или отсчета) 0-0.

Правила выбора плоскости отсчета 0-0 и определения величин z · Плоскость 0-0 всегда проходит горизонтально. · Для удобства её проводят через центр тяжести одного из сечений. · Высота положения центра тяжести сечения z выше плоскости отсчета считается положительной, а ниже – отрицательной.

В нашей задаче проводим плоскость 0-0 горизонтально через центр тяжести второго сечения. Она совпадает с сечением 2-2.

Итак:

Неизвестная величина – давление р₁ вычисляется из уравнения Бернулли. Все остальные величины, входящие в уравнение, или известны по условию, или определяются.

2. Определяем слагаемые уравнения Бернулли в общем виде (не вычисляя). Далее подставляем их в уравнение Бернулли, приводим подобные члены, производим алгебраические преобразования и определяем из этого уравнения неизвестную величину (силу R) в общем виде.

· Высоты центров тяжести сечений: z₁ = - H₀; z₂ =0;

· Средние скорости в сечениях : J₁ = Q/w₁ =4× Q/p/D²;

J₂ = Q/w₂. Так как w₂ >> /w₁, то J₂ << J₁ и можно принять J₂ =0.

Правила определения скоростей J₁ и J₂ · Средняяскорость в сечении равна расход / площадь: J = Q/w. (34) · Если площадь одного из сечений много больше площади другого сечения, то скорость в этом сечении будет много меньше скорости в другом сечении и её можно принять равной нулю. Это следует из закона постоянства расхода жидкости: J₁×w₁ = J₂×w₂=.......=Q = const.

· Коэффициенты Кориолиса a₁ и a₂ зависят от режима движения жидкости. При ламинарном режиме a =2, а при турбулентном a =1.

· Абсолютное давление в первом сечении р₁ = р_1м + р_ат, р_1м – избыточное (манометрическое) давление в первом сечении, оно неизвестно и подлежит определению. Давление р_1м можно связать с силой R через условие равномерного движения поршня.

 

Таким образом, при известной силе R можно определить манометрическое давление и, наоборот, зная манометрическое давление, можно вычислить силу.

· Абсолютное давление во втором сечении р₂ = р_м0 + р_ат.

После подстановки абсолютных давлений в уравнение Бернулли атмосферное давление сократится.

Правила определения абсолютных давлений р₁ и р₂ в центрах тяжести сечений · Абсолютное давление в центре тяжести сечения определяется через показания р_м или р_v приборов (мановакуумметров): р = р_м + р_ат, если р > р_ат; р = - р_v + р_ат, если р < р_ат. При этом атмосферное давление входит в левую и правую часть уравнения Бернулли и сокращается. Это неудивительно. Параметры гидродинамического процесса не должны зависеть от атмосферного давления! · Если известна внешняя сила, действующая на поршень, давление можно определить из условия: алгебраическая сумма всех сил равна нулю. И наоборот, зная давление, можно определить внешнюю силу.

· Потери напора h_1-2 складываются из потерь напора на трение по длине потока h_дл и потерь на местные гидравлические сопротивления å h_м:

h_1-2 = h_дл + å h_м.

Определение потерь по длине трубопровода h_дл 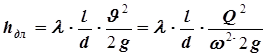, - формула Дарси-Вейсбаха (35) · где l, d, w - длина, диаметр и площадь поперечного сечения трубопровода; · J, Q – средняя скорость и расход в сечении трубопровода; · l - коэффициент гидравлического трения. Последовательность вычисления коэффициента трения l · Определяется режим движения жидкости, для чего вычисляется безразмерное число Рейнольдса: 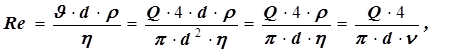(36) где h и n = h/r - соответственно динамический и кинематический коэффициенты вязкости[4], приводятся в справочной литературе (Приложение 1). · Вычисленное значение числа Рейнольдса Re сравнивается с критическим значением Re_кр. Если Re < Re_кр – имеет место ламинарный[5] режим. Если Re > Re_кр – имеет место турбулентный[6] режим. Критическое число Рейнольдса зависит от формы поперечного сечения канала. Для круглого сечения Re_кр =2300. При ламинарном режиме (Re < 2300): l= 64 / Re. (37) При турбулентном режиме (Re >2300): l = 0,11 ×( 68 /Re + D_э/d)^0,25, (38) где D_э – эквивалентная шероховатость поверхности трубопровода, зависит от материала поверхности и способа её обработки, приводится в справочниках (Приложение 5).

В нашей задаче потери по длине необходимо записать так:

.

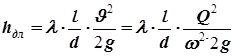Далее необходимо определить местные[7] гидравлические сопротивления, возникающие при движении жидкости от сечения 1-1 к сечению 2-2. Обычно зона деформации потока в районе местного сопротивления невелика по сравнению с длиной труб. Поэтому считают, что местные потери имеют место как бы в одном сечении, а не на участке, имеющем некоторую длину.

Местные гидравлические сопротивления всегда возникают в тех сечениях потока, где скорость движения резко меняется по величине или по направлению. Согласно этому, в нашей задаче (Рис.16) имеют место сопротивление при внезапном сужении потока (выход из цилиндра в трубопровод) - h_{вн.суж .}, при прохождении жидкости через вентиль – h_в, в двух резких поворотах на угол 90° - 2 h_{пов .}, и при резком расширении потока при выходе из трубы в бак - h_вых.

å h_м = h_{вн.суж .} + h_в + 2 h_{пов .} + h_вых

Дата добавления: 2015-05-23