Кавитационный расчет сифона

Графический способ решения

Решить любое уравнение - это значит найти то значение неизвестной величины, при котором левая часть уравнения равна правой.

Графический способ основан на построении графиков функций левой и правой частей уравнения (46) и нахождении точки их пересечения. При этом последовательно задаются рядом значений диаметра d, вычисляя при каждом значении d число Re, l, f(d), F(d). В данном случае F(d) обозначена левая часть уравнения (46).

Последовательность вычисления коэффициента трения l накаждом шагеостается прежней, а именно:

Последовательность вычисления l:

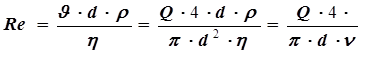
	Re < 2300	l= 64 / Re
	Re > 2300	l = 0,11 ×( 68 /Re + Dэ/d)^0,25

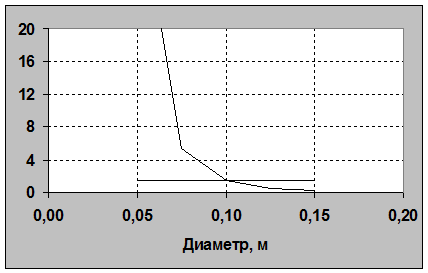
Ниже представлена расчетная таблица и графики, выполненные на ЭВМ с помощью электронных таблиц (Microsoft Excel).

d	0,05	0,075	0,10	0,13	0,15
Re	4,63E+04	3,09E+04	2,32E+04	1,85E+04	1,54E+04
l	2,50E-02	2,57E-02	2,68E-02	2,79E-02	2,90E-02
f(d)	37,4644	5,35238	1,38307	0,49048	0,21179
F(d)	1,38	1,38	1,38	1,38	1,38

Явление кипения жидкости при давлениях меньших атмосферного и равных давлению насыщенного пара, при нормальных температурах (10°, 20°,30°,.....),сопровождающееся схлопыванием пузырьков пара в областях повышенного давления, называется кавитацией.

Давление насыщенного пара зависит от рода жидкости и температуры (Приложение 8).

Рис. 21

Зависимость давления насыщенного пара воды от температуры

На рисунке показана зависимость насыщенного пара воды от температуры. Примерно такой же вид имеет такая зависимость для других жидкостей. Для того, чтобы вода закипела при 20°С, необходимо создать очень низкое давление – 2300Па.

Кавитация - вредное явление. Рассмотрим следствия кавитации на примере работы сифона.

Пузырьки пара, выделяющиеся при кавитации, разрывают межмолекулярные связи, поток жидкости при этом теряет сплошность, столб жидкости на восходящей линии сифона и процесс всасывания прекращается. Кроме того, пузырьки пара, продвигаясь вместе с жидкостью дальше на нисходящую линию сифона, где давление больше давления насыщенного пара, лопаются.

При схлопывании пузырька на твердой поверхности трубы жидкость, устремившаяся в освободившееся пространство, останавливается. При этом ее кинетическая энергия превращается в потенциальную и происходят местные гидравлические удары. Это явление сопровождается существенным ростом давления и температуры и приводит к разрушению материала поверхности.

Поскольку давление насыщенного пара при обычных температурах меньше атмосферного, сечения, где давление меньше атмосферного, считаются опасными с точки зрения возникновения кавитации.

В инженерной практике существует правило:

Не допускать кавитации!

Для этого необходимо, чтобы в сечениях потока, где давление меньше атмосферного, было выдержано условие: давление в жидкости больше давления насыщенного пара.

р > p_н.п.. (47)

Это условие отсутствия кавитации.

Проверяем условие нормальной работы сифона

Для этого необходимо определить давление в опасном сечении 3-3 и сравнить его с заданным по условию давлением насыщенного пара жидкости.

1. Определяем давление в сечении 3-3 из уравнения Бернулли, составленного для сечений 1-1 и 3-3.

,

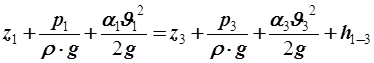где:

· р₁ и р₃ – абсолютные давления в центрах тяжести сечений;

· J₁ и J₃ – средние скорости в сечениях;

· z₁ и z₃ – высоты центров тяжести сечений относительно плоскости отсчета 0-0;

· h_1-3 –потери напора при движении жидкости от первого до второго сечения.

2. Определяем слагаемые уравнения Бернулли в данной задаче.

· Высоты центров тяжести сечений: z₁ = 0; z₂ = h₀;

· Средние скорости в сечениях: J₃ = Q/w=4×Q/p/d²;

J₁ = Q/w₁. Так как w₁>>/w₃, то J₁ <<J₃ и можно принять J₁ =0.

· Коэффициенты Кориолиса a₁ и a₂ зависят от режима движения жидкости. При ламинарном режиме a =2, а при турбулентном a =1.

· Абсолютное давление в первом сечении р₁ = р_ат,

· Абсолютное давление в сечении 3-3 неизвестно и подлежит определению..

· Потери напора h_1-3 складываются из потерь напора на трение по длине потока h_дл и потерь на местные гидравлические сопротивления å h_м:

h_1-3 = h_дл + å h_м.

· Потери по длине равны:

,

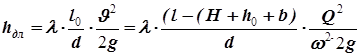где l₀ – длина трубопровода от начала до сечения 3-3. l₀ = 50-(1,38+3+2) = 43,62;

· местные потери напора равны:

å h_м = å x₀× J²/( 2 g) = å x₀× Q²/(w²× 2 g); где å x₀ = x_ф + x_пов.

x_ф =1,7; x_пов = 0,23; (Приложение 6).

å x₀ = 1,7 + 0,23 =1,93.

· Суммарные потери напора равны:

h_1-2 = (l×l₀/d+åx₀) × Q²/(w²× 2 g).

Итак, подставляем определенные выше величины в уравнение Бернулли.

В нашей задаче закон сохранения энергииимеет вид:

.

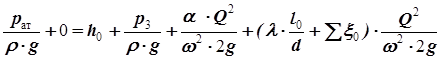Убираем нули, приводим подобные члены и выражаем давление р₃.

В результате получим:

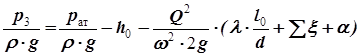. (48)

Из уравнения (48) определяем давление р₃. Значение коэффициента трения определено ранее и равно 0,0268 (см. таблицы), a = 1 (режим турбулентный), w=p×d² /4 = 3,14×0,1²/4=7,85×10^-3м².

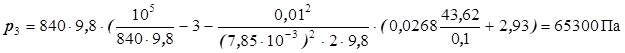
Давление насыщенного пара равно 2 кПа. Так как 65,3 >> 2, то сифон будет работать.

Дата добавления: 2015-05-23