Критерій Пірсона

Перевірка гіпотези про узгодженість розподілів

Розрізняють два види задач перевірки гіпотез про узгодженість розподілів: порівняння отриманого емпіричного розподілу з деяким теоретичним та порівняння двох емпіричних розподілів. Задача першого типу виникає як правило тоді, коли для статистичної обробки результатів спостережень необхідно використати параметричний критерій. У цьому випадку нам апріорі потрібна інформація про вид розподілу отриманих даних. Для цього здійснюється порівняння емпіричного розподілу з одним з теоретичних. Задача другого типу виникає, наприклад, у випадку класифікації спостережуваних явищ. Узгодженість емпіричних розподілів двох явищ дає підстави віднести їх до одного класу, а неузгодженість — до різних класів.

Для перевірки гіпотези про узгодженість розподілів найчастіше використовують 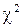критерій Пірсона.

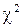критерій Пірсона застосовується як для перевірки узгодженості емпіричного розподілу із заданим теоретичним, так і для перевірки узгодженості емпіричних розподілів. Критерій є непараметричним.

У першому випадку критерій служить для перевірки наступних гіпотез:

Н ₀: розподіл ознаки збігається із заданим теоретичним;

Н ₁: ознака розподілена за відмінним від заданого законом.

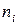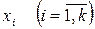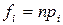Якщо — емпірична частота варіанти , а , де 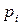— ймовірність , а — об’єм вибірки, то величину

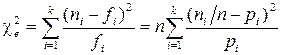
називають емпіричним значенням 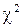критерію Пірсона. Критичну точку для заданого рівня значущості α і ν ступенів вільності визначають з таблиць критичних значень розподілу 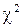(таблиця 4 додатка) або в EXCEL за формулою =ХИ2ОБР(α;ν)).

Кількість ступенів вільності ν визначають за формулою

,

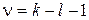де k — кількість варіант, l — кількість незалежних параметрів розподілу, які визначаються за вибіркою.

Якщо 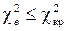для рівня значущості 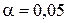, то приймається гіпотеза Н ₀, у випадку, коли для рівня значущості , приймається альтернативна гіпотеза Н ₁.

Приклад 20. Групі учнів 10–11 класів (90 чоловік) пропонували впорядкувати за важливістю такі риси ідеального учня: І — акуратність, ІІ — самостійність, ІІІ — уважність, ІV — творчість, V — допитливість, VI — активність, VII — обов'язковість, VIII — наполегливість, ІХ — сміливість, Х — відкритість, ХІ — почуття гумору, ХІІ — товариськість, ХІІІ — рішучість, XIV — впевненість у своїх діях, XV — дружелюбність. Результати впорядкування подано в таблиці:

І

ІІ

ІІІ

ІV

V

VI

VII

VIII

IX

X

XI

XII

XIII

XIV

XV

Чи можна стверджувати, що учні не надавали переваги уважності? Чи можна те ж саме стверджувати про наполегливість?

Розв’язання: Якщо наше припущення правильне, то вибір даної ознаки мав би рівномірно розподілитись між п’ятнадцятьма місцями, тобто на кожне місце припало б по шість виборів. Розрахуємо емпіричне значення 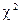критерію Пірсона.

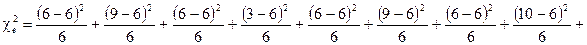
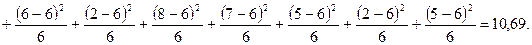
Кількість ступенів вільності дорівнює 15 – 1 = 14. Критичні значення для ν = 14 і α = 0,05 та α = 0,01, відповідно дорівнюють та 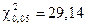. Оскільки, 10,69 < 23,68, то приймається нульова гіпотеза, яка стверджує, що розподіл виборів ознаки за місцями статистично не відрізняється від рівномірного, тобто в характеристиці ідеального учня опитувані не надали переваги цій ознаці.

Розрахуємо емпіричне значення 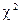критерію для восьмої ознаки

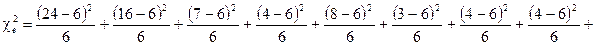
Оскільки, 90,33 > 29,14, то розподіл восьмої ознаки за 15 місцями нерівномірний. Можна стверджувати, що більшість опитаних віддавали перевагу цій ознаці ідеального учня.

Для неперервного розподілу порівнюємо емпіричні і теоретичні частоти попадання значень досліджуваної величини у відповідні класи.

Зазначимо, що в цьому випадку статистика 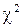тим точніше апроксимується 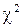розподілом Пірсона, чим більші є теоретичні частоти у кожному класі. Як правило, вимагається, щоб частоти в кожному класі були не менші, ніж 5. А це іноді вимагає укрупнення класів.

Приклад 21. Чи можна стверджувати, що час, затрачений учнями на розв’язування поставленої задачі (приклад 16), розподілений за нормальним законом?

Розв’язання: Об’єм вибірки п = 124. Побудуємо інтервальний варіаційний ряд, розбивши проміжок [8,195) на 11 інтервалів:

[8; 25)	[25; 42)	[42; 59)	[59; 76)	[76; 93)	[93; 110)	[110; 127)	[127; 144)	[144;161)	[161;178)	[178; 195)

Оскільки на деяких інтервалах частоти менші, ніж 5, то зробимо укрупнення крайніх інтервалів:

[8; 25)	[25; 42)	[42; 59)	[59; 76)	[76; 93)	[93; 195)

Вибіркове середнє та оцінка стандартного відхилення відповідно дорівнюють . Теоретичні частоти для інтервалу знаходимо за формулою 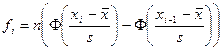. Отже, для заданих проміжків

	[8; 25)	[25; 42)	[42; 59)	[59; 76)	[76; 93)	[93; 195)
ni
fi	13,4	21,4	25,9	23,8	16,6	13,5

Обчислимо емпіричне значення критерію .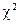

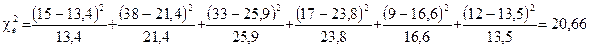Кількість ступенів вільності 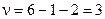, бо накладено дві додаткові в’язі для визначення 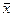та s. Критичні значення критерію відповідно дорівнюють 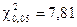та 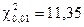. Оскільки 20,66 > 11,35, то гіпотеза про те, що час розв’язання задачі розподілений за нормальним законом з параметрами , відхиляється.

У випадку перевірки узгодженості двох (чи кількох) емпіричних розподілів 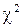критерій Пірсона служить для перевірки наступних гіпотез:

Н ₀: закони розподілів ознак не відрізняються між собою;

Н ₁: ознаки розподілені за різними законами.

Гіпотеза Н ₀ у цьому випадку фактично означає, що вибірки належать до однієї генеральної сукупності, тому в якості теоретичних частот у критерії 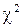беруть усереднені за сукупністю вибірок частоти. Кількість ступенів вільності визначається за формулою 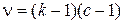, де k — кількість розрядів ознаки, с — кількість розподілів, що порівнюються.

Приклад 22. За методикою Спілберга опитано дві групи віруючих: формально віруючі християни (ФВХ) та практикуючі християни (ПХ). Розподіл рівня особистісної тривожності у цих групах подано в таблиці.

	Низький	Середній	Високий
ПХ
ФВХ

Чи можна стверджувати, що рівень особистісної тривожності в обох групах розподілений однаково?

Розв’язання: Сформулюємо статистичні гіпотези для нашої задачі.

Н ₀: Відмінності у розподілах рівнів особистісної тривожності є випадковими.

Н ₁: Відмінності у розподілах рівнів особистісної тривожності закономірні.

Вибірка практикуючих християн містить 33 елементи, а формально віруючих християн — 37 елементів. Тому у припущенні, що вибірки отримані з однієї генеральної сукупності, теоретичні частоти розраховуються так:

	Низький	Середній	Високий
ПХ
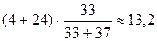
ФВХ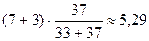

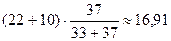
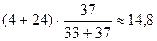
Обчислимо значення статистики .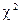

Кількість ступенів вільності 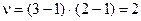. Знаходимо критичні значення критерію: 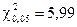, . Оскільки 20,22 > 9,21, то нульова гіпотеза відхиляється. Можемо стверджувати, що відмінності у розподілі рівнів особистісної тривожності в обох групах мають закономірний характер, зокрема у групі формально віруючих християн переважає високий рівень особистісної тривожності.

Дата добавления: 2015-05-23