Критерій Колмогорова

Критерій Колмогорова застосовують для перевірки узгодженості емпіричного розподілу деякої випадкової величини із заданим неперервним теоретичним розподілом, тобто для перевірки гіпотез:

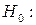розподіл ознаки збігається з даним теоретичним;

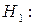ознака розподілена за відмінним від заданого законом.

Критерій ґрунтується на зіставленні нагромаджених емпіричних і теоретичних частот (кумулянт). Статистикою виступає величина

,

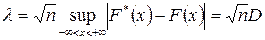де 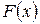— гіпотетична функція розподілу досліджуваної випадкової величини, 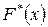— емпірична функція розподілу. Критична область — правостороння. Статистика виражає максимальну розбіжність між емпіричною і теоретичною функціями розподілу, що дозволяє оцінити узгодженість розподілів поточково.

Якщо справджується нульова гіпотеза, то для достатньо малих проміжків інтервального варіаційного ряду і для достатньо великого обсягу вибірки статистика D має граничний розподіл, який не залежить від функції F, а саме

,

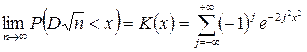що дозволяє визначати критичні значення 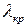(а відповідно і 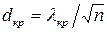) для заданого рівня значущості 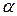з наближеного рівняння

.

Зокрема для 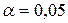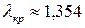, а для .

Якщо емпіричне значення статистики 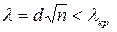, то з надійністю приймається гіпотеза , в іншому випадку приймається альтернативна гіпотеза .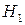

Приклад 23. Чи можна стверджувати, що час, затрачений учнями на розв’язування поставленої задачі (приклад 16), розподілений за логнормальним законом?

Розв’язання: Логнормальний розподіл з параметрами а та 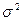задається щільністю

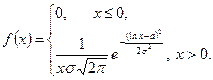
Враховуючи, що для логнормального розподілу математичне сподівання і дисперсія пов’язані з параметрами розподілу рівностями 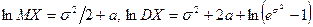, та оцінки 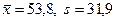(див. приклад 21), знаходимо значення 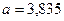та .

Висуваємо гіпотези:

спостережувані затрати часу мають логнормальний розподіл з параметрами 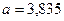та ;

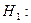розподіл спостережуваних затрат часу відмінний від логнормального.

Об’єм вибірки п = 124. Розбивши додатну піввісь на 11 інтервалів обчислимо емпіричні відносні частоти, значення емпіричної і теоретичної функцій розподілу для верхніх меж проміжків та їх різниці.

інтервал	(0; 25)	[25; 42)	[42; 59)	[59; 76)	[76; 93)	[93; 110)	[110; 127)	[127; 144)	[144;161)	[161;178)	[178; +¥)
пі
	0,121	0,306	0,266	0,137	0,073	0,032	0,008	0,032	0,016		0,008
	0,121	0,427	0,693	0,831	0,903	0,935	0,944	0,976	0,992	0,992
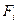
	0,131	0,430	0,671	0,817	0,898	0,943	0,967	0,981	0,988	0,993
	0,010	0,003	0,022	0,014	0,005	0,008	0,023	0,005	0,004	0,001

Таким чином емпіричне значення і 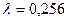. Оскільки 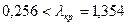, то на рівні значущості 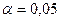приймаємо гіпотезу , яка стверджує що даний розподіл збігається з логнормальним.

Дата добавления: 2015-05-23