Критерій Смирнова

Критерій Смирнова дозволяє на підставі двох серій незалежних спостережень 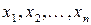та перевірити гіпотезу про те, що результати спостережень в обох серіях отримані з випробувань над величинами з однаковою функцією розподілу (порівняти два емпіричні розподіли). Статистичні гіпотези формулюються так:

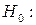задані емпіричні розподіли збігаються;

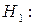задані емпіричні розподіли істотно відрізняються.

Для перевірки гіпотез використовують статистику Смирнова

,

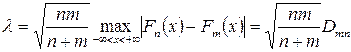де і — емпіричні функції розподілу першої і другої серій спостережень відповідно.

Розподіл статистики Смирнова не залежить від виду функції розподілу і є протабульованим для малих т і п. Критична область визначається нерівністю

,

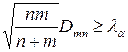де 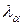— квантиль розподілу статистики Смирнова, що відповідає рівню значущості 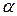. Для досить великих т і п критичне значення 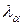знаходимо із співвідношення .

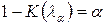Приклад 24. [*]Тест Мюнстерберга (в адаптивному варіанті Дворяшиної М.Д.) вимірювання вибірковості перцептивної уваги пропонувався студентам факультету психології Ленінградського університету (156 чол.) та акторам балету Маріїнського театру (85 чол.). Методика полягає в тому, що серед розміщених у довільному порядку букв на бланку досліджуваний повинен якнайшвидше знайти і підкреслити 24 слова різного рівня складності. Емпіричні розподіли кількості пропущених слів наведено в таблиці.

	Кількість пропущених слів
Студенти
Актори

Чи можна стверджувати, що ці розподіли однакові?

Розв’язання: Формулюємо статистичні гіпотези.

Н ₀: Емпіричні розподіли кількості пропущених слів у тесті статистично не відрізняються між собою.

Н ₁: Емпіричні розподіли кількості пропущених слів у тесті істотно відмінні.

Для їх перевірки знайдемо відносні частоти емпіричних розподілів, нагромаджені відносні частоти та їх різниці.

Пропущено слів	Відносні частоти	Нагромаджені відносні частоти	Різниці
Студенти	Актори	Студенти	Актори
	0,596	0,259	0,596	0,259	0,337
	0,173	0,235	0,769	0,494	0,275
	0,071	0,188	0,840	0,682	0,157
	0,096	0,047	0,936	0,729	0,206
	0,032	0,035	0,968	0,765	0,203
	0,019	0,129	0,987	0,894	0,093
	0,013	0,035	1,000	0,929	0,071
	0,000	0,035	1,000	0,965	0,035
	0,000	0,024	1,000	0,988	0,012
	0,000	0,012	1,000	1,000	0,000

Максимальне відхилення нагромаджених відносних частот (кумулянт) дорівнює 0,337. Отже, статистика Смирнова 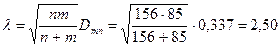. Відповідні критичні зна­чення: 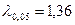та 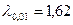. Як бачимо, емпіричне значення статистики потрапляє в критичну область. Отже, приймаємо альтернативну гіпотезу, яка стверджує, що розподіли кількості пропущених слів у студентів університету і акторів істотно відмінні.

У пакеті STATISTICA 6.0 перевірка гіпотези про узгодженість розподілу з даним теоретичним розподілом реалізується модулем Distribution Fitting. Дані спостережень заносимо в одну змінну. Із пропонованого модулем списку вибираємо вид теоретичного розподілу. Параметри розподілу визначаються модулем автоматично. Результати перевірки відповідних гіпотез для прикладів 21 і 23 можна побачити на рис. 17. Висновок про прийняття чи відхилення нульової гіпотези у кожному з цих випадків робимо за величиною рівня значущості р емпіричного значення відповідного критерію (приймаємо нульову гіпотезу, якщо 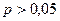і відхиляємо її та приймаємо альтернативну гіпотезу, якщо ).

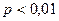Дата добавления: 2015-05-23