Перевірка гіпотези про рівність двох дисперсій

Перевірку гіпотези про рівність дисперсій двох нормально розподілених генеральних сукупностей на основі вибірок з них здійснюють за допомогою критерію Фішера. Оцінками дисперсій генеральних сукупностей слугують обчислені за вибірками з них незміщені оцінки 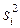. В цьому випадку статистичні гіпотези формулюються так.

Н ₀: Дисперсії нормально розподілених генеральних сукупностей рівні.

Н ₁: Дисперсія генеральної сукупності з більшою незміщеною оцінкою дисперсії більша від дисперсії генеральної сукупності, представленої іншою вибіркою.

Статистика Фішера

,

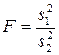де 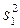— більша, а 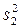— менша з незміщених оцінок дисперсій генеральних сукупностей за вибірками, при виконанні нульової гіпотези має розподіл Фішера-Снедекора з 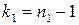, ступенями вільності. Критичну точку правосторонньої критичної області для рівня значущості 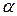знаходять за таблицями критичних значень розподілу Фішера-Снедекора (таблиця 5 додатка) або в EXCEL за формулою =FОБР(α; k ₁; k ₂).

Приклад 25. Порівняти дисперсії розподілу кількості пропущених слів групою акторів та групою студентів за даними попереднього прикладу.

Розв’язання: Формулюємо статистичні гіпотези.

Н ₀: Дисперсії розподілів кількості пропущених слів у тесті статистично не відрізняються між собою.

Н ₁: Дисперсія з більшою незміщеною оцінкою більша.

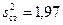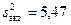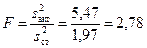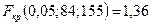Обчислимо незміщені оцінки дисперсій для кожної з вибірок: , . Відношення Фішера . Але , а 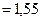, тому обчислене емпіричне значення критерію Фішера потрапляє у критичну область. Нульова гіпотеза відхиляється, приймається гіпотеза Н ₁.

Дата добавления: 2015-05-23