Метод дотичних

Нехай ф-я f(x) двічі неперервно диф-на на в-ку [a;b], при чому f^’(x), f^’’(x) 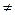0 і зберігає свій знак на цьому відрізку. Нехай корінь відокремлений на в-ку [a;b].

Суть методу дотичних полягає в тому, що криву у= f(x) заміняємо дотичною до цієї кривої, проведеної у кінцях відрізка. Точка перетину дотичної з віссю Ох вважається наближенням до розв’язку рівняння.

Проведемо дослідження методом дотичних на І типі кривої. Дотичну будемо проводити до кривої у= f(x) на тому кінці відрізка [a;b], де значення функції f(x) і 2-ї похідної f^’’(x) співпадають за знаком.

Позначимо точку перетину першої дотичної з віссю Ох с₁, яку будемо вважати першим наближенням до кореня 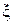. Знайдемо координату першого наближення. Для цього запишемо рівняння дотичної проведеної до графіка функції у= f(x) в точці В(b,f(b)).

у- f(b)= f`(b)(х- b)

Позначимо координати першого наближення у=0, х=с₁.

- f(b)= f`(b)(с₁- b)→ .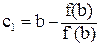

Неперервний корінь рівняння знаходиться на відрізку [a;с₁]. Проведемо дотичну до графіка функції у правому кінці відрізка. Тоді формула знаходження другого наближення с₂ матиме вигляд

.

В результаті одержимо загальну формулу знаходження n–го наближення

.

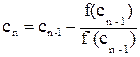Суть комбінованого методу хорд і дотичних полягає в тому, що з одного кінця ми будуємо хорди, а з другого дотичні. Цей метод має вищу швидкість збіжності ніж методи хорд і дотичних окремо взяті.

Малюнок №2

2. Уточнення наближених значень коренів рівняння f (x)=0 методом ітерацій. Геометрична ілюстрація. Блок-схема методу. Достатня умова збіжності методу ітерацій для рівнянь з одним невідомим. Оцінка похибки методу ітерацій для рівнянь з одним невідомим.

Нехай задано рів-ня f(x)=0 при чому корінь цього р-ня відокремлений на в-ку [a;b], а ф-я f(x) неперервна на цьому відрізку. Замінимо дане рів-ня рів-ням , при чому функція неперервно диференційована на в-ку [a;b].

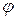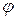Суть методу ітерації полягає в тому, що ми вибираємо на відрізку [a;b] початкове наближення х₀. наступні наближення будемо обчислювати за рекурентною формулою х_n= (x_n-1), n=1,2,… Якщо послідовна наближеність {x_n}є збіжною, тобто має границю lim x_n=c, то це є коренем рівняння f(x)=0, а також рівносильного йому рівняння . Дійсно с=lim x_n=lim (x_n-1)= 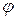(lim x_n-1)= 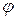(c). Збіжна послідовність {x_n} забезпечується вибором функції та початковим наближенням х₀. якщо х₀ вибрати ближче до кореня то швидкість збіжності підвищується, а вибираючи по різному функцію можна одержати різні ітераційні процеси знаходження кореня рівняння =0.

Достатні умови збіжності методу ітерацій:

Т: Нехай функція f(x) визначена і неперервна на відрізку [a;b]

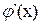| |≤q<1. Всі послідовні наближення x_n, які визначаються за рекурентною формулою x_n= 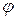(x_n-1) не виходять за межі інтервала [a;b]. Тоді послідовна наближеність x_n є збіжною, при чому границя послідовності є єдиним коренем рівняння f(x) = 0 і справджується оцінка

.

Геометричний зміст методу ітерацій

Побудуємо графіки функцій у=х і у= . Розглянемо 4 випадки:

І <1

II >1

III <-1

IV >-1

I Вибираємо точку х₀. х_n=φ(x_n-1) і отримаємо В₁, опускаємо перпендикуляр і отримаємо х₁. А₀(х₀,х₀), В₁(х₁, φ(x₁)), А₁(х₁,х₁), В₂(х₂, φ(x₂)), А₂(х₂,х₂), В₃(х₃, φ(x₃)).(Графік 1)

ІІ Вибираємо х₀, проведем вісь паралельну Оу, потім паралельну Ох – утвориться точка В₁. кореня немає, іде розбіжність. (Графік 2)

ІІІ Вибираємо точку х₀ ближче до ξ, піднімаємо перпендикуляр вверх – утвориться точка А₀. Горизонтально проводимо пряму – утвориться точка В₁, якій відповідає х₁. х₀, х₁,..., х_n віддаляється від кореня – немає збіжності. (Графік 3)

IV Вибираємо х₀, піднімаємо перпендикуляр до перетину з прямою у=х. Це буде точка А₀. Проводимо паралельну осі Ох і утворилась точка В₁, опускаємо перпендикуляр – одержуємо х₁. х₀, х₁,... послідовно наближуються до кореня. (Графік 4)

Дата добавления: 2015-05-23