Розв’язування систем алгебраїчних рівнянь методом ітерацій. Достатня умова збіжності методу ітерацій для систем алгебраїчних рівнянь та оцінка похибки методу

Класифікація методів роз-ня систем. Точні методи роз-ня систем лін. алгебраїчних р-нь(СЛАР). Роз-ня СЛАР методом Гауса та уточнення коренів, одержаних цим методом. Погано обумовлені с-ми р-нь.

Розглянемо систему з n рівнянь і n невідомих:

a₁₁x₁+ a₁₂x₂+…+ a_1nx_n=b₁

a₂₁x₁+ a₂₂x₂+…+ a_2nx_n=b₂ (1)

…

a_n1x₁+ a_n2x₂+…+ a_nnx_n=b_n.

Cистему (1) можна записати у вигляді:

, j=1,…,n 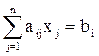, i=1,…,n

Розв’язком с-ми(1) називається упорядкований набір (с₁, с₂,..., с_n) чисел, після підстановки яких в систему(1) кожне рівняння перетворюється у тотожність.

Методи розв’язання СЛАР можна поділити на: *Точні; * Наближені.

До точних методів належать метод Гаусса, метод квадратних коренів, метод Крамера, матричний метод.

Метод називається наближеним або ітераційним, якщо він дає змогу знайти наближений розв’язок системи(1) із наперед заданою точністю зі шляхом виконання скінченої кількості арифметичних операцій.

Метод Гаусса (метод послідовного виключення невідомих). За цим методом розв’язуємо СЛАР у два етапи:

· На першому етапі вихідну систему зводять до рівносильної їй системи східчастого вигляду. Цей процес перетворення називається прямим входом.

· На другому етапі, що називається зворотнім ходом знаходимо розв’язок одержаної системи.

a₁₁x₁+ a₁₂x₂+ a₁₃x₃=а₁₄

a₂₁x₁+ a₂₂x₂+ a₂₃x₃=а₂₄ (2)

a₃₁x₁+ a₃₂x₂+a₃₃x₃=а_34.

Припустимо, що система є сумісню і визначена, тобто ∆≠0. Нехай коефіцієнт а₁₁≠0, тоді виключимо змінну х₁ із 2-го і 3-го рівняння системи (2). Для цього перше рівняння поділимо на коефіцієнт a₁₁, одержимо:

х₁+а₁₂⁽¹⁾х₂+ а₁₃⁽¹⁾х₃= а₁₄⁽¹⁾, де 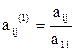, j=2,3,4.

Верхній індекс означає порядок перетворення рівняння. Домножимо перше рівняння на а_і1 і віднімемо його від 2-го і 3-го рівняння відповідно. В результаті одержимо систему 2-х рівнянь:

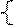а₂₂⁽¹⁾х₂+ а₂₃⁽¹⁾х₃= а₂₄⁽¹⁾

а₃₂⁽¹⁾х₂+ а₃₃⁽¹⁾х₃= а₃₄⁽¹⁾, де а_ij⁽¹⁾=a_ij-a_1j⁽¹⁾a_i1, i,j=2,3,4. (3)

Виконаємо аналогічні перетворення із системою (3). Поділимо перше рівняння на а₂₂⁽¹⁾

х₂+ а₂₃⁽²⁾х₃= а₂₄⁽²⁾, де 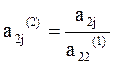, j=3,4.

Виключимо х₂ з 2-го рівняння системи (3): помножимо одержане рівняння на а₃₂⁽¹⁾ і віднімемо від 2-го рівняння:

сх₃= а₃₄⁽²⁾, а_3j⁽²⁾=a_3j⁽²⁾-a_2j⁽¹⁾a₃₂⁽¹⁾, j=3,4.

Знайдемо х₃ з останнього рівняння:

х₃= а₃₄⁽³⁾,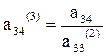

В результаті одержимо систему східчастого вигляду:

х₁+а₁₂⁽¹⁾х₂+ а₁₃⁽¹⁾х₃= а₁₄⁽¹⁾,

х₂+ а₂₃⁽²⁾х₃= а₂₄⁽²⁾, (4)

х₃= а₃₄⁽³⁾.

Система (4) рівносильна системі (2), оскільки ми використали елементарні перетворення рівнянь. Прямий хід завершено, при чому елементарні перетворення можна виконати, якщо a₁₁≠0, а₂₂⁽¹⁾≠0, а₃₃⁽²⁾≠0.

Метод простої ітерації. Розглянемо с-му з n рівнянь з n невідомими:

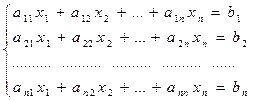(1)

Представимо с-му у матричному вигляді: A 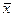= 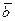(2)

Нехай всі елементи 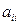(і= 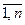) матриці А відмінні від 0. Залишимо в лівій частині р-ня с-ми діагональні елементи і кожне р-ня поділимо на 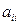одержимо: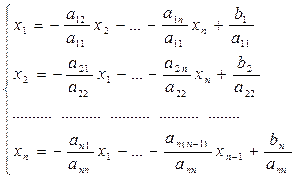

Запишемо с-му у матричній формі:

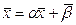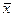( - це вектор стовпець) (3)

α=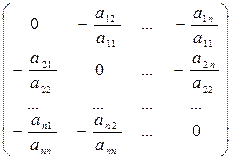

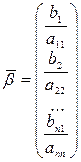
С-му (3) наз. зведеною с-мою послідовного наближення для відшукання розв. с-ми (3) будують за формулами:

(4)

За початкові наближення 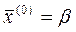, як правило обирають вільні члени. Якщо послідовність 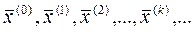є збіжною, то границя є розв. с-ми (3).

Праву частину с-ми (3) можна розглядати, як деяке відображення. Оператор φ, який відображає вектор 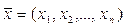в n-вимірному просторі у вектор 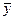, який визначається за формулою: 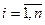. Тоді відшукання розв.с-ми (3) зводиться до відшукання нерухомої точки відображення φ. (Нерух. т. 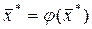). Якщо відображення φ є стискуючим, то розв. р-ня 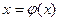можна знайти за методом послідовних наближень з довільним поч. вектором. Розглянемо випадки при яких відображення φ буде стискуючим. Поняття стискуючого оператора залежить від самого оператора, а також від вибору метрики n-вимірного простору. Розглянемо 3 випадки вибору метрики:

1.Нехай відстань між векторами 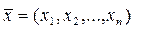і 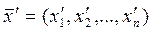визнач. за формулою:

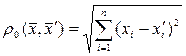Знайдемо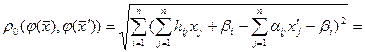

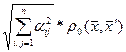
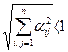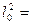
Отже, оператор φ буде стикуючим, коли , 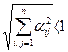(5)

Якщо 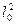<1,то з принципу стискуючих відображень р-ня (3) має єдиний корінь.

2. Нехай метрику введемо за формулами: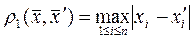

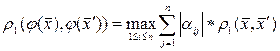
Відображення φ буде стискуючим, якщо викон. нер-сть:

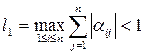(6)

Якщо ум(6) викон.,то за прин-м стискуючого відоб-ня(3) буде мати єдин.розв.

3. Визначимо відстань між 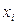та 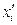за допомогою формули: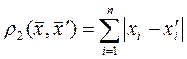

(7)

Якщо умова (7) викон., то відобр. φ є стискаючим і за принципом стискаючого відображення р-ня (3) має єдиний корінь.

Т1. Якщо матриця α с-ми р-нь (3) задовольняє одну з умов (5)-(7) (0<l₁<1, 0<l₂<1, 0<l₃<1), то с-ма (3) має єдиний розвязок 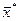, який можна знайти, як границю 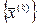, побудованої за допомогою рекурентних формул (4) почин. з довільного поч. наближення .

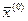Т2. Якщо елементи матриці А задов. одну з умов:

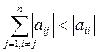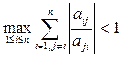, , , то с-ма р-нь (1) має єдиний розв. 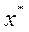, який можна одержати, як границю послідовності 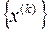побудованої за формулами:

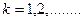
Починаючи з довільного початкового наближення .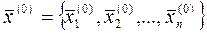

Оцінка похибки методу простої ітерації визнач ф-лою: 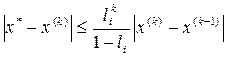, де визнач. за формулою (5), (6), (7).

Дата добавления: 2015-05-23