Нормований метричний простір

Надалі ми будемо використовувати поняття лінійної системи, яке розглядалося в лінійній алгебрі.

Означення 2.1. Непорожня множина Χ називається лінійною системою над полем Р, дійсних чисел, якщо:

I.Для будь-яких двох елементів хÎR і уÎR є однозначно визначений третій елемент z=x+y, який називається їх сумою, причому

1) х+у=у+х (комутативність додавання),

2)х+(у+z)=(x+y)+z (асоціативність додавання).

II.Для будь-якого дійсного числа a і будь-якого елемента х Î R існує і притому єдиний елемент aх, який називається добутком елемента х на число a, причому (a і b - числа, х, у - елементи):

3) a(bх)=(ab)х (асоціативність множення),

4)1^. х = х,

5) a(х+у)= a х+ a у (дистрибутивність множення

6) (a+b)х=aх+bх відносно додавання).

III.Існує такий елемент q ÎR, який називається нульовим, що

7) 0 х =q для будь-якого хÎR.

Означення 2.1. Лінійний система Х називається лінійним нормованимпростором, якщо 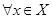ставиться у відповідність дійсне число 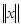, яке задовільняє наступним умовам:

1) 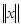≥0, причому 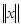=0 тоді і тільки тоді, коли ;

2) , 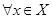виконується рівність ;

3)для довільних з множини виконується нерівність

Число 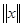називається нормою елемента х. Елементи множини називаються точками, або векторами простору.

Якщо в лінійному нормованому просторі за відстань між елементами х, у прийняти

(2.1),

то отримаємо метричний простір.

Дійсно, з умови 1) означення 1.3 випливає, що , причому 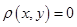тоді і тільки тоді, коли , а це еквівалентно тому, що . Так, як 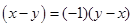, то з умови 2) означення 1.3 маємо

.

Виконання умови 3) означення метричного простору слідує з властивості 3) означення 2.1. Дійсно нехай 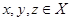, тоді

.

Таким чином ми переконались, що будь-який лінійний нормований простір стає метричним простором, якщо покласти 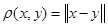. При цьому слід зауважити, що .

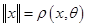Зауваження 1.1 Якщо маємо лінійну систему і на ній введена матрика, то не завжди величину 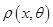можна прийняти за 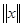. Справді, розглянемо множину S всіх послідовностей дійсних чисел 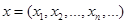. Коли відстань між двома послідовностями 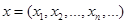і , визначимо рівністю , то множина S стане метричним простором. Якщо в цьому просторі ввести поняття суми х+у і добутку a х, елементів х на дійсне число a, як це робиться з послідовностями, а за нульовий елемент прийняти q=(0,0,...,0), то даний метричний простір стане лінійною системою. Коли за значення норми елемента х прийняти число , то не буде виконуватись друга аксіома норми, тобто не завжди дорівнює

Дата добавления: 2015-05-24