Скалярний добуток

Означення 3.1. Нехай маємо лінійну систему Х. Говорять, що на лінійній системі Х введено скалярний добуток, якщо будь-якій парі елементів і 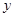із цієї системи ставиться у відповідність дійсне число 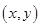, яке задовільняє наступним умовам:

1)(х,у)=(у,х);

2)(х+у,z)=(x,z)+(y,z);

3) для довільного дійсного числа 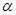і довільних 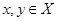виконується рівність (a х,у)=a(х,у);

4)(х,х)³0 причому (х,х)=0 тоді і тільки тоді коли х= q.

Число (х,у) називають скалярним добутком елементів х і у. З означення скалярного добутку випливає:

, .

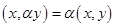Позначимо . Пізніше ми покажемо, що ця величина задовольняє всім умовам норми.

Теорема 3.1. Нехай Х – лінійна система, на якій введено скалярний добуток. Тоді для будь-яких 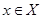і 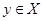має місце нерівність

(3.1)

Нерівність (3.1) називається нерівністю Коші-Буняковського.

Доведення. Якщо 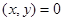, то нерівність (3.1) очевидна.

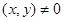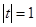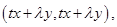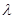Розглянемо випадок, коли . Нехай , очевидно, . Розглянемо скалярний добуток де λ – довільне дійсне число. Внаслідок означення скалярного добутку (умова 4) при довільному . Перетворивши вираз, який стоїть в лівій частині нерівності одержим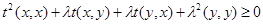о: , або . Оскільки квадратний тричлен при всіх дійсних 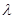невідє’мний, то дискримінант цього тричлена недодатній, тобто звідси і слідує нерівність (3.1).

Покажемо, що величина 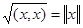є нормою. Виконання умови 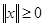, очевидне. Причому тоді і тільки тоді, коли . Це слідує із умови 4) означення скалярного добутку. З рівності 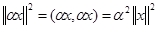, де 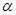– дійсне число, слідує, що . Переконаємось, що 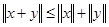. Так, як ,

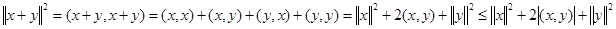то внаслідок нерівності (3.1) маємо: 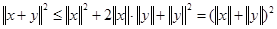. Звідси слідує: 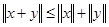. Нерівність доведена.

Таким чином ми бачимо, що лінійна система, на якій введено скалярний добуток, стає лінійним нормованим простором, якщо норму визначити рівністю , а значить і метричним, якщо за відстань між елементами х і у прийняти величину .

Дата добавления: 2015-05-24