Лабораторна робота №2

Опис схеми устаткування.

Устаткуванням для виконання лабораторної роботи є комп’ютерний клас.

Контрольні питання

1 В чому проявляються особливості ієрархічних систем управління.

2 Охарактеризуйте основні класи задач управління.

3 Назвіть типові функціональні структури систем управління.

4 В чому особливості координатного, параметричного та структурного управління.

5 Наведіть приклади різних цілей систем управління.

6 Які способи компенсації збурень застосовуються складних системах управління?

7 В чому полягають особливості систем із змінюваною структурою?

«АНАЛІЗ ЕРГОДИЧНОСТІ В СИСТЕМАХ КЕРУВАННЯ ВИПАДКОВИХ ПРОЦЕСІВ»

Мета, завдання і тривалість роботи.

МЕТА: ознайомитись з методологією перевірки гіпотези ергодичності випадкових процесів.

ЗАВДАННЯ: визначити ергодичність конкретного випадкового процесу, заданого викладачем.

ТРИВАЛІСТЬ РОБОТИ: 2 академічні години.

Основні теоретичні положення

Аналіз ергодичності випадкових процесів є актуальною науково-практичною задачею у зв’язку з необхідністю мати вірогідну інформацію про статистичні характеристики процесу на всьому періоді роботи об’єкта, а не на обмеженій ділянці. Особливе значення ця проблема має для складних об’єктів, що функціонують під впливом завад за умов апріорної та поточної невизначеності щодо структури та параметрів об’єкта.

Для оцінки точності лінійних систем автоматичного контролю і керування при розв’язанні багатьох прикладних задач достатньо знати перші два моменти випадкового процесу: математичне сподівання і автокореляційну функцію. Ці характеристики є невипадковими функціями і являють собою результат ймовірнісного усереднення різних функцій випадкового процесу. Властивості статистичних процесів, що визначаються двома першими моментами, вивчаються за допомогою кореляційної теорії.

Якщо автокореляційна функція R _xx(τ) наближено зменшується за модулем при │ τ │→ ∞, та стаціонарна випадкова функція х (t) ергодична. Властивість ергодичності дуже важлива для вирішення багатьох практичних задач автоматизації процесів контролю і керування [2], оскільки для ергодичних процесів статистичні характеристики, які отримані усередненням по часу однієї реалізації наближено співпадають з характеристиками, отриманими усередненням по множині реалізацій. Тобто, спостереження випадкового процесу на одному об’єкті протягом тривалого часу дає в середньому таку ж саму картину, як і значна кількість спостережень, проведених в один і той ж момент часу на великій кількості об’єктів одного типу. Це дає змогу для визначення статистичних характеристик обмежитися одним дослідом досить великого інтервалу часу, тобто обмежитися обробкою однієї реалізації замість множини дослідів, необхідних для визначення характеристики процесу, не маючого властивостей ергодичності. Особливе значення і актуальність це має для аналізу статистичних властивостей показників такого нетипового невідтворюваного випадкового процесу як процес буріння нафтових і газових свердловин.

При розробці пристроїв для автоматизованого контролю механічної швидкості можливі два методи: вимірювання величини проходки за заданий проміжок часу і вимірювання інтервалу часу, витраченого на певну проходку. Для оцінки доцільності застосування одного із цих методів для конкретних способів буріння (роторного, турбінного, електробуріння), глибини свердловини, геологічних структур необхідно знати статистичні характеристики механічної швидкості.

Для вирішення цієї задачі необхідно оцінити ергодичність процесу, для чого треба знати автокореляційну функцію механічної швидкості R _vv(τ).

У зв’язку з тим, що механічна швидкість є нестаціонарною випадковою функцією, при оцінюванні її автокореляційної функції важливим є питання вибору необхідної довжини реалізації Т_р, яка забезпечує потрібну точність обчислення автокреляційної функції R _vv(τ). У нашому випадку для виключення похибки від нестаціонарності висунута вимога

Т_р < Т_ст ,

де Т_ст – інтервал станціонарності, який визначається різницею математичних сподівань на сусідніх ділянках і; і +1:

│ М_v (t_i) - М_v (t_i+1)│ < δ,

де δ – допустима величина відхилення.

Отже, верхня межа довжини реалізації Т_р визначена інтервалом стаціонарності випадкової функції механічної швидкості V (t), а нижня – допустимою похибкою обчислення автокореляційної функції R _vv(τ), що визначається дисперсією оцінки R _vv(τ), яка зменшується із збільшенням довжини реалізації Т_р. Для одержання вірогідної інформації про властивості випадкової функції V (t) довжину реалізації Т_р. і крок дискретизації Δ t можна вибирати, користуючись ще однією умовою:

Т_р ≥ (10÷20) Т_нч,

Δ t ≤ 0,5 Т_вч,

де Т_нч – період низькочастотної складової сигналу V (t);

Т_вч – період високочастотної складової сигналу V (t),

а також виразом:

,

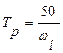отриманим за допомогою розкладання випадкової функції в ряд Фурьє.

Тут ω_н – нижча частота ряду Фурьє.

Кількість відліків ординат у цьому випадку можна визначати з виразу

,

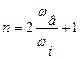де ω_в – верхня частота ряду Фурьє.

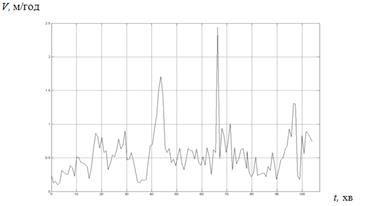
Рисунок 2.1. Графік зміни механічної швидкості V (t) в часі

Як видно з графіка V (t), механічна швидкість має стохастичний характер.

Для знаходження математичного сподівання М_v, дисперсії Д_v і автокореляційної функції R _vv(τ) провели дискретизацію графіка V (t) з кроком дискретизації Δ t = 0,84 с і скористались стандартними функціями програмного продукту Matlab6,5 у вигляді:

М 1 = mean (T) – математичне сподівання;

Д 1 = (S 1)^2 – дисперсія;

S 1 = std (T) – середньоквадратичне відхидення.

Отримано такі результати: М_v =0,5468 м/год; Д_v = 0,1142 м²/год²; S_v = 0,3379 м/год.

Для визначення автокореляційної функції і спектральної густини скористаємось формулами:

, ,

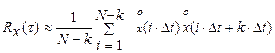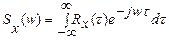На рис.2.2 і рис 2.3 наведені графіки нормованих автокореляційних функцій R _vv(τ) і спектральної густини S_vv (ω), отриманих за результатами емпіричних досліджень.

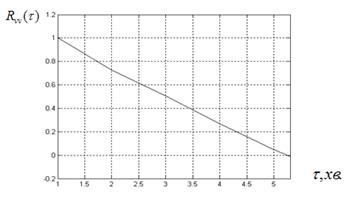
Рисунок 2.2. Графік нормованої автокореляційної фукнції R _vv(τ)

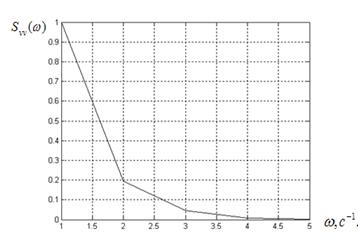
Рисунок 2.3. Графік нормованих значень спектральної густини механічної швидкості S_vv (ω)

Аналогічні графіки автокореляційних функцій R _vv(τ) отримані при різних значеннях початкової механічної швидкості: М_v = 20 м/год., М_v = 7 м/год., М_v = 1 м/год. Встановлено, що параметри отриманих нормованих автокореляційних функцій залежать від середніх значень механічної швидкості, що зв’язано з нестаціонарністю функції швидкості буріння V (t). Із збільшенням середнього значення швидкості збільшується дисперсія Д_vv=R _vv(0), але зменшується інтервал кореляції τ_о.

Значення параметрів апроксимуючого виразу

,

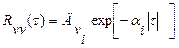який отримали за методом найменших квадратів, для різних значень математичного сподівання М_v наведено в таблиці 2.1.

Таблиця 2.1 Параметри апроксимуючої формули

Статистичні характеристики	Розмірність	Варіанти
а	б	в
Мv	м/год		7,0
Дv	м^2/год^2	20,1	6,8	0,44
α	1/хв	0,69	0,43	0,23

За результатами експериментальних досліджень, проведених на буровій № 522 ГС була також досліджена ергодичність таких випадкових процесів як зміни осьової сили Р на бурове долото в часі, струму І двигуна електробура Е240-8, його активної потужності N іоцінки відносного зношення долота Е. Після дискретизації сигналів P (t), I (t), N (t), E (t) з кроком дискретизації 0,84с, були отримані масиви, які були оброблені за допомогою розроблених програм в середовищі програмного продукту Matlab 6.5. Отримані такі результати (табл.2.2).

Автокореляційна функція і спектральна густина кожного досліджуваного випадкового процесу визначались за формулами.

Таблиця 2.2. Статистичні характеристики випадкових процесів P (t), I (t), N (t), E (t)

Статистичні характеристики   Процес	Мате-матичне сподівання	Середньо-квадра-тичне відхилен-ня	Диспер- сія
P (t)	104,91	2,58	6,66
I (t)	143,03	7,22	52,24
N (t)	234,60	2,43	5,91
E (t)	2,59	1,70	2,88

В результаті виконання програми обробки експериментальних даних отримано графіки нормованих автокореляційних функцій і спектральної густини, які наведені на рис. 2.4, рис.2.5.

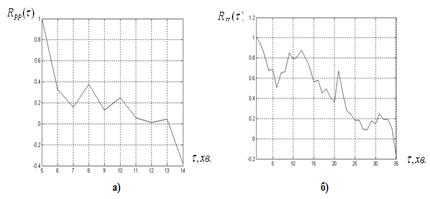
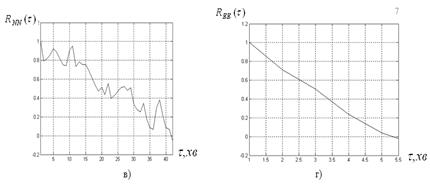
Рисунок 2.4. Графіки нормованих автокореляційних функцій

а) сигналу P (t) – R_pp (τ); б) сигналу І (t) – R_іі (τ);

в) сигналу N (t) – R_NN (τ); г) сигналу Е (t) – R_ЕЕ (τ).

Нормалізація дозволяє співставити автокореляційні функції незалежно від того, рівні або відрізняються середньоквадратичні відхилення.

Нормовані спектральні гістини представлені на графіках нижче (рис.2.5).

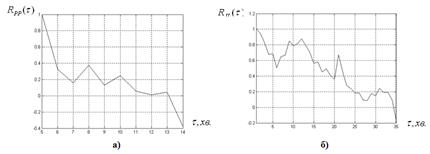
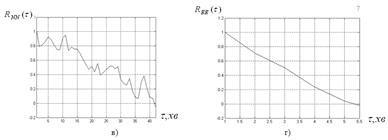
Рисунок 2.5. Графіки нормованих автокореляційних функцій

а) сигналу P (t) – R_pp (τ); б) сигналу І (t) – R_іі (τ);

в) сигналу N (t) – R_NN (τ); г) сигналу Е (t) – R_ЕЕ (τ).

Нормалізація дозволяє співставити автокореляційні функції незалежно від того, рівні або відрізняються середньоквадратичні відхилення.

Нормовані спектральні гістини представлені на графіках нижче (рис.2.6).

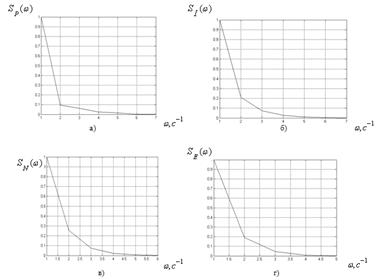
Рисунок 2.6. Графіки нормованих значень спектральних густин: а) сигналу P (t); б) сигналу І (t); в) сигналу N (t); г) сигналу Е (t)

Аналіз графіків нормованих автокореляційних функцій R_vv (τ), R_pp (τ), R_іі (τ), R_NN (τ), R_ЕЕ (τ) (рис.3, рис.6) дозволив визначити час кореляції – відрізок на осі τ, за межами якого автокореляційна функція практично дорівнює нулю.

Час кореляції τ _кор. визначили із умови, що значення нормованої автокореляційної функції 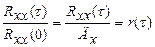стає при τ > τ _кор. менше достатньомалого числа γ = 0,1. Отримані результати наведені в таблиці 2.3.

Таблиця 2.3. Час кореляції для досліджуваних випадкових процесів

	Rpp (τ)	Rіі (τ),	RNN (τ),	Rvv (τ)	RЕЕ (τ)
τ кор.				6.2	5.3

Отже, проведений аналіз автокореляційних функцій довів, що розглянуті випадкові процеси є ергодичними.

Для всіх розглянутих функцій виконуються умови:

R_xx (0) ≥ │ R_xx (τ)│, (2.12)

де R_xx (0) = D_xx > 0.

R_xx (∞) = 0; (2.13)

R_xx (τ) = R_xx (- τ). (2.14)

Автокореляційні функції осьової сили R_pp (τ), струму двигуна електробура R_іі (τ), активної потужності R_NN (τ), містять періодичну складову, що говорить про те, що випадкові функції P (t), I (t), N (t) також містять періодичну складову цієї ж частоти. Причиною виявлених коливань є спосіб подачі бурильного інструменту на вибій свердловини. Найбільшу крутизну мають криві автокореляційних функцій R_ЕЕ (τ) і R_vv (τ). Це означає, що випадкові процеси V (t), Е (t) містять більш високі частоти ніж інші процеси. Це обумовлено конструкцією трьохшарошкових доліт і швидкістю їх обертання.

Визначені графіки для R_xx (τ) і S (ω) дозволяють визначити наступні властивості отриманих спектральних густин:

1 Якщо автокореляційні функції R_ЕЕ (τ) і R_vv (τ) монотонні спадаючі функції τ, то S_v (ω) i S_Е (ω) теж монотонні спадаючі фукнції.

2 Широким графікам R_РР (τ) і R_іі (τ) автокореляційних функцій відповідають вузькі графіки спектральної густини S_Р (ω) i S_І (ω).

3 Оскільки при τ= 0 для будь-якої центрованої випадкової функції х (t) автокореляційна функція рівна

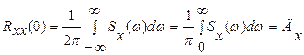, (2.15)

то дисперсія кожної розглянутої стаціонарної випадкової функції V (t), P (t), I (t),

N (t) пропорційна площі, обмеженої кривими спектральними густинами S_v (ω),

S_Е (ω), S_Р (ω), S_І (ω) і S_N (ω) і віссю абсцис.

4 Будь-яка з розглягутих автокореляційних функцій може бути апроксимована з бажаним степенем точності рядом, членом якого є степеневі функції:

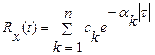. (2.16)

Нами запропоновано [5] використовувати більш просту і зручну для апрокмисмації аналітичну модель

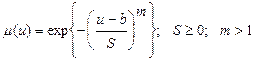. (2.17)

Якщо прийняти b =0 і задавати S =1,2,…, і т.д., а також m =1,2,4, то можна отримати широку гамму функцій.

Аналітична модель кореляційної функції, завдяки неперервності і диференційованості є більш зручною для використання не етапі аналізу статистичних властивостей випадкових процесів.

Спектральна густина, яка відповідає функції (2.16) може бути визначена за формулою:

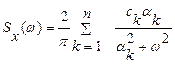. (2.18)

Це дозволяє спростити апроксимацію експериментально отриманих графіків автокореляційних функцій і спектральних густин.

Висновок. Експериментальними і теоретичними дослідженнями доведено, що випадкові процеси зміни механічної швидкості буріння V (t), осьової сили на долото Р (t), струму електробура І (t), активної потужності двигуна електробура N (t), оцінки відносного зношення оснащення долота Е (t) є ергодичними випадковими процесами, оскільки їх автокореляційні функції R_vv (τ), R_РР (τ), R_іі (τ), R_NN (τ), R_ЕЕ (τ) зменшуються за модулем при │ τ │→ ∞.

Отримані статистичні характеристики досліджених процесів можуть бути використані при розробці пристроїв автоматичного контролю цих параметрів процесу буріння нафтових і газових свердловин, для вибору кроку дискретизації сигналу в системах автоматизованого контролю і захисту керованого об’єкта від аварійних ситуацій.

Дата добавления: 2015-05-24