Лабораторна робота № 5. Порядок виконання роботи

Порядок виконання роботи

Опис схеми установки

Увстаткуванням до виконання лабораторної роботи №4 є комп’ютерний клас.

1. Ознайомитись з метою і завданням лабораторної роботи.

2. Вивчити основні теоретичні положення щодо формування шкал лінгвістичних термів.

3. Згідно індивідуального завдання викладача сформувати шкалу для лігнвістичного терму.

4. Зробити висновок відносно отриманого результату.

Методичні рекомендації щодо виконання

лабораторної роботи

Основні формули для обчислення і довідкову інформацію слід використати із основних теоретичних положень (пункт 1.). Результати формування шкали оформити у вигляді звіту.

Контрольні запитання

1.Скільки варіантів побудови нечітких каналів спостереження дозволяє використати нечіткий підхід?

2. Які переваги нечітких каналів спостереження?

3. Які складності використання нечітких каналів спостереження?

4. За якою формулою визначають кількість термів для формування шкали?

5. Яка модель найбільш зручна для опису лінгвістичних змінних?

«АНАЛІЗ ТА ВИБІР ФОРМИ ФУНКЦІЙ НАЛЕЖНОСТІ ДЛЯ ФАЗИФІКАЦІЇ ВХІДНИХ СИГНАЛІВ СИСТЕМ КОНТРОЛЮ І УПРАВЛІННЯ»

Мета, завдання і тривалість роботи.

МЕТА: вивчити методи вибору форми функцій належності для фазифікації вхідних сигналів систем контролю і управління.

ЗАВДАННЯ: визначити похибку апроксимації заданої функції належності по відношенню до трикутної.

ТРИВАЛІСТЬ РОБОТИ: 2 академічні години.

1.Основні теоретичні положення

Існуючі моделі об’єктів та систем контролю і управління не відповідають сучасному рівню інформаційного забезпечення нафтогазовидобувних підприємств. Проте, побудова математичних моделей складних технологічних процесів і об’єктів нафтової і газової промисловості суттєво ускладнена тим, що:

• об’єкти моделювання нестаціонарні і випадкові, функціонують за умов апріорної та поточної невизначеності і перебувають під впливом зовнішніх завад, розвиваються в часі і характерузуються великою кількістю і складністю зв’язків між параметрами стану;

• традиційні методи опису технологічних процесів ведуть до таких складних математичних конструкцій, що стає неможливим їх практичне використання; тут доречно згадати висловлення проф. Л.А.Заде про те, що по мірі того, як складність зростає, точні твердження втрачають значимість, а значимі ствердження втрачають точність;

• не всі технологічні параметри можливо виміряти з потрібною точністю, а частину параметрів взагалі неможливо контролювати.

Одним із шляхів подолання вказаних труднощів є використання для моделювання якісної інформації у вигляді лінгвістичного опису технологічного процессу за допомогою нечітких термів. Формалізувати терми словесного опису технологічного процессу дозволяє методологія теорії нечітких множин, згідно якої кожному терму словесного опису ставиться у відповідність, так звана, нечітка множина А у деякому пристрої Х, що позначається А Х, тобто:

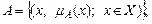
де 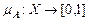– функція належності множини А.

Ця функція приписує кожному елементу 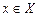ступінь йогоо належності до нечіткої множини А. При цьому можливі три випадки:

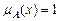• означає повну належність елемента х до нечіткої множини А, тобто ;

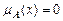• означає відсутність належності елемента х до нечіткої множини А, тобто ;

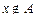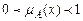• означає часткову належність елемента х до нечіткої множини А.

Оскільки при контролі технологічних параметрів Х – це простір з кінцевою кількістю елементів, тобто 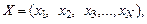то нечітка множина А Х може бути записана у такому вигляді:

.

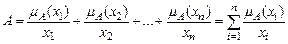В прикладних задачах контролю використовуються стандартні форми функцій належності: класів s, p, 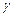, t, L та інші. Вибір форм функцій належності (ФН) для фазифікації вхідних сигналів від давачів технологічних параметрів об’єктів, що функціонують за умов апріорної та поточної невизначеності і перебувають під впливом зовнішніх завад, є актуальною задачею у зв’язку з інтенсивним впровадженням в системи контролю і управління, що розробляються для нафтової і газової промисловостей, методів теорії нечітких множин і нечіткої логіки.

Аналіз літературних джерел показує, що у загальному випадку форма функцій належності та її параметри можуть бути сформовані із застосуванням різних методів: методу статистичної обробки експертної інформації, методу парних порівнянь, вдосконаленого методу парних порівнянь Сааті, або при використанні стандартних функцій належності та їх аналітичного запису.

Проте, результатами проведеного аналізу встановлено:

• методологія статистичної обробки експертної інформації припускає наявність досить високої похибки, яка досягає 30% і залежить від професійного рівня експертів;

• при використанні вдосконаленого методу парних порівнянь Сааті в систему вводиться додаткова похибка, яка пов’язана з наближеним зведенням отриманої ФН до стандартного виду з аналітичною формою запису;

• вдосконалений метод парних порівнянь Сааті дозволяє отримати графічну форму функцій належності, однак, при використанні традиційної технології нечітких множин необхідна досить проста аналітична форма запису.

Виділення невирішених частин

Отже, аналіз літературних джерел показує недостатній об’єм проведених досліджень в напрямку використання формальних критеріїв оцінки і вибору форми ФН та їх порівняння. Особливе значення це має для створення інформаційних моделей нечітких систем контролю технічних параметрів в нафтогазовидобувній галузі, а саме для контролю і управління процесом буріння, де технологічні параметри, як правило, мають великі розмахи і двохпараметричні закони розподілу.

Метою даної роботи є оцінювання похибок апроксимації гаусоподібної, дзвоноподібної та експоненціальної ФН за допомогою трикутних або трапецієподібних форм ФН, використання яких є більш доцільним в модулях фазифікації систем контролю і управління, що створюються для об’єктів нафтогазової промисловості.

Функція Гауса задається такою формулою:

(5.1)

де 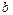- координати максимуму функції; 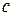- кількісна характеристика концентрації функції.

Тобто, коефіцієнт 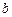показує на скільки зміщений максимум функції відносно початку координат, а 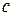- швидкість зростаня і спаданя функції 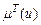. Зобразимо функцію (5.1) при 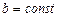і .

В зв’язку з тим, що реалізовувати таку функцію є тяще чим, наприклад, лінійну функцію, виникає потреба апроксимувати дану функцію лінійною, як показано на рис. 5.1.

Рисунок 5.1. Графік функції Гауса при різних с

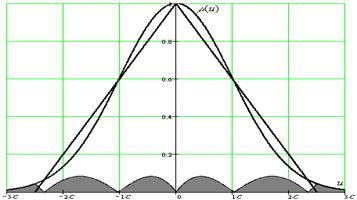
Рисунок 5.2. Апроксимований трикутником графік функції Гауса

Залита область – це похибка апроксимації. Її необхідно визначити. Визначати будемо інтегральним методом. Припускаємо, що 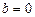, оскільки цей коефіцієнт не впливає на похибку.

Нам необхідні аналітично задані функці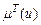ї і 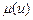. Функція 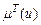є задана (5.1), а функцію 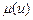необхідно аналітично описати, виходячи з графіка на рис. 5.2. Опишемо її умовною лінійною функцією, яка проходить через три точки: (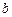;1),(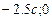), ()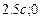. Знайшовши вирази прямих, які проходять через ці точки, запишемо функцію :

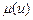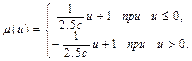(5.2)

Отже, маючи дві функці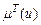ї і 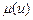, знайдемо точку їх перетину, де абсолютна похибка змінює свій знак на протилежний. Для цього необхідно розв’язати систему з двох рівнянь. Розглядаємо тільки праву частини графіка (рис. 5.2), бо функці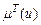ї і 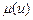є симетричні відносно осі :

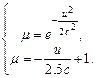(5.3)

З другого рівняння виражаємо , підставляємо його в перше і логарифмуємо ліву та праву частини:

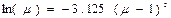. (5.4)

Рівняння (4) розв’язуємо в Mathcad:

.

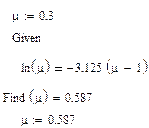
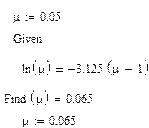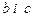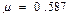Отже, ми отримали, що при будь-яких значеннях , функції (5.1) і (5.2) перетинаються в точці з ординатами і . Виразимо з другого рівняння системи (3) :

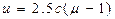. (5.5)

Підставивши знайдені значення 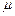, отримаємо залежність координати точки перетину функцій від коефіцієнта с: , . Отже, для того, щоб знайти абсолютну похибку апроксимації, нам необхідно взяти такий інтеграл:

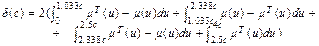. (5.6)

Знайшовши в програмному пакеті Mathcad інтеграл (5.6), отримуємо залежність абсолютної похибки апроксимації від коефіцієнта :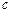

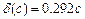. (5.7)

Отже, як видно з рівняння (5.7), залежність похибки апроксимації від коефіцієнта 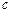є лінійною і похибка буде тим менша, чим меншим буде коефіцієнт .

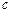Проведемо аналогічно апроксимацію експоненціальної і дзвоноподібної функцій.

Експоненціальна функція задається виразом:

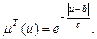(5.8)

Апроксимуємо експоненціальну функцію лінійною, як показано на рис. 5.3.

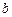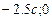Визначаємо координати точок, через які проходить трикутна функція: (;1),() і (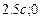). Знайшовши вирази прямих, які проходять через ці точки, запишемо умовну функцію :

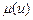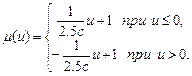(9)

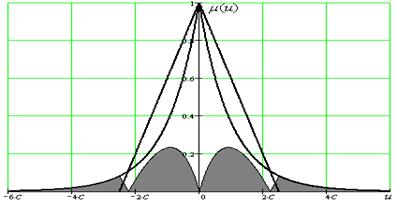
Рисунок 5.3. Апроксимований трикутником графік експоненціальної функції

Отже, маючи дві функці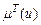ї і 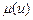, знайдемо точку їх перетину де абсолютна похибка змінює свій знак на протилежний. Для цього необхідно розв’язати систему з двох рівнянь:

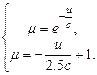(5.10)

З другого рівняння виражаємо , підставляємо його в перше і логарифмуємо:

. (5.11)

Рівняння (5.11) розв’язуємо в Mathcad. Отже, ми отримали, що при будь-яких значеннях 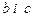функції (5.8) і (5.9) перетинаються в точці з ординатою 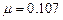. Виразимо з другого рівняння системи (5.10) :

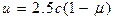. (5.12)

Підставивши знайдене значення 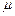, отримаємо залежність координати точки перетину функцій від коефіцієнта с. 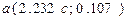. (5.13)

Отже, для того, щоб знайти абсолютну похибку апроксимації, нам необхідно обчислити такий інтеграл:

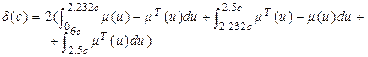. (5.14)

Знайшовши в програмному пакеті Mathcad інтеграл (5.14), отримуємо залежність абсолютної похибки апроксимації від коефіцієнта :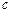

. (5.15)

Дзвоноподібна функція задається виразом:

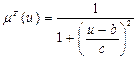. (5.16)

Апроксимуємо дзвоноподібну функцію лінійною, як показано на рис.5.4.

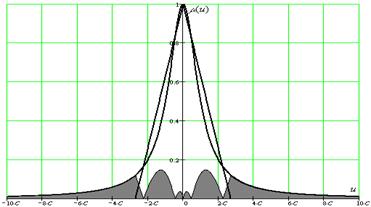
Рисунок 5.4. Апроксимований трикутником графік дзвоноподібної функції

Координати точок, через які проходить трикутна функція: (b;1), (-2,5c; 0) і (2,5с; 0). Запишемо умовну функцію :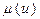

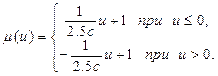(5.17)

Отже, маючи дві функці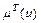ї і 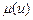, знайдемо точку їх перетину де абсолютна похибка змінює свій знак на протилежний. Розв’язуєм систему з двох рівнянь:

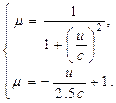(5.18)

З другого рівняння виражаємо 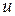і підставляємо його в перше:

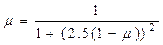. (5.19)

Розв’язавши рівняння (19) в Mathcad, отримаємо 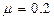і . Виразимо з другого рівняння системи (5.19) : 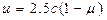. Підставивши знайдене значення 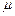, отримаємо залежність координат точки перетину функцій від коефіцієнта с: , 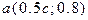. Отже, для того щоб знайти абсолютну похибку апроксимації нам необхідно обчислити такий інтеграл:

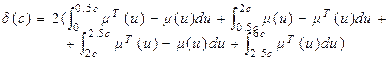(5.20)

Знайшовши в програмному пакеті Mathcad інтеграл (5.20), отримуємо залежність абсолютної похибки апроксимації від коефіцієнта с: 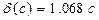. Проаналізувавши графіки на рис.5.2, рис.5.3, рис.5.4, бачимо, що функцію Гауса можна апроксимувати також трапецевидною функцією. Здійснимо цю апроксимацію на рис.5.5:

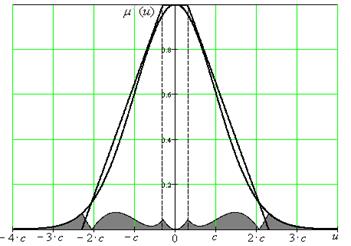
Рисунок 5.5. Апроксимований трапецією графік функції Гауса

Опишемо трапецію умовною лінійною функцією, яка проходить через чотири точки: (-0.3с;1),(0.3с;1) і точки (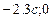),(). Записавши вирази прямих [6], які проходять через ці точки, запишемо умовну функцію :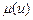

(5.21)

Отже, маючи дві функці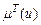ї і 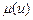, знайдемо точку їх перетину, де абсолютна похибка змінює свій знак на протилежний. Для цього необхідно розв’язати систему з двох рівнянь:

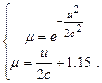(5.22)

З другого рівняння виражаємо і підставляємо в перше, після чого логарифмуємо: 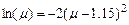. Рівняння розв’язуємо в Mathcad. Отримуємо, що 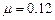. Виразимо з другого рівняння системи (5.22) : 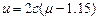. Підставивши знайдене значення 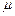, отримаємо залежність точки перетину функцій від коефіцієнта с: .

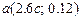Отже, для того, щоб знайти абсолютну похибку апроксимації нам необхідно взяти в програмному пакеті Mathcad інтеграл:

.

Отримуємо залежність абсолютної похибки апроксимації від коефіцієнта с: .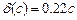

Отже, залежність похибки апроксимації від коефіцієнта 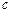є лінійною і похибка буде тим менша, чим меншим буде коефіцієнт .

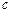Проаналізуємо отримані результати інтегральних оцінок похибки апроксимації трикутною функцією функцій Гауса, експоненціальної і дзвоноподібної, а також трапецевидною функцією функцію Гауса:

- апроксимація функції Гауса трикутною функцією;

- апроксимація експоненціальної функції трикутною функцією;

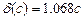- апроксимація дзвоноподібної функції трикутною функцією;

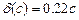- апроксимація функції Гауса трапецевидною функцією.

Висновки: на основі аналізу похибок апроксимації, проведеного за величиною коефіцієнтів при с, встановлено, що за результатами інтегральної оцінки найкраще апроксимується трикутною і трапецієвидною функцією належності функція Гауса, при чому, кращі результати дає апроксимація трапецієвидною функцією; для фазифікації сигналів, що характеризують технологічні процеси в нафтовій і газовій промисловості (буріння свердловин, видобування, транспортування, зберігання нафти і газу), можна рекомендувати функції належності класів L, 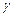, t і трапецієвидну.

Вказівки щодо виконання лабораторної роботи

Для підготовки до заняття слід ознайомитись з основними теоретичними положеннями, які викладені в пункті 1 даної лабораторної роботи.

Дата добавления: 2015-05-24