Однопродуктовая статическая модель без дефицита

Детерминированные модели

Эту модель можно интерпретировать как модель управления запасами в магазине. Для упрощения задачи рассматривается только один товар. Руководство магазина закупает товар у оптовиков по цене c₁ за единицу товара, если объем закупаемой партии y меньше величины q. В случае, если объем закупаемой партии больше или равен q, делается скидка и цена единицы товара становится равной c₂ < c₁. Затраты при закупке товара состоят из двух величин: условно постоянной величины (например, аренды автомобиля для доставки товара от оптового склада до магазина) будем называть ее стоимостью оформления заказа, и обозначать буквой K; переменной величины ¾ стоимости закупаемой партии равной c(y)y. Здесь c(y) равно c₁,если y < q и равно c₂, если y ³ q. В рассматриваемой модели предполагается, что в магазине спрос на товар в единицу времени является величиной постоянной и принимает значение, равное b.

Магазин также несет расходы по хранению товара на собственном складе. В каждую единицу времени (час, день и т.д.) эти расходы составляют величину h за каждую единицу товара, находящуюся на складе в эту единицу времени. Можно интерпретировать эту величину как стоимость «омертвления средств» в виде товарного запаса.

После оформления заказа товар поступает на склад магазина через интервал времени длиной t^*.

Руководству нужно определить, какое количество y товара заказывать, и точку заказа R с тем, чтобы суммарные затраты в единицу времени на закупку продаваемого товара и хранение товара на складе было минимальным.

Будем считать, что величина y меняется непрерывно. Это допущение при большом объеме товара не является жестким ограничением. Затраты в рассматриваемом случае будут состоять из суммы трех величин: затрат на приобретение продаваемого товара, затрат на оформление заказа, затрат на хранение товара на собственном складе.

Можно показать [3, с. 9 – 11], что при минимальных затратах новая партия поступает на склад магазина в момент, когда весь товар израсходован. Следовательно, максимальное количество товара на складе равно y в момент поставки. График зависимости количества товара на складе от времени показан на рис. 2. Ось x ¾ ось времени, а ось y ¾ значение величины запаса на складе.

Вычислим средние затраты в единицу времени S(y). Отметим, что это можно сделать для одного периода [0; D1], так как на остальных периодах все вычисления будут полностью совпадать.

В момент t=0 на складе имеется максимальное количество запаса, равное y. В единицу времени расходуется b единиц запаса, следовательно, весь запас будет израсходован за время

t = y/b. (1)

y

B

A C F

R

0 E G D1 D2 D3 t

Рис. 1

За рассматриваемое время заказ будет оформляться один раз, а расходы на оформление заказа в единицу времени составят

K/ t = Kb/y. (2)

Так как величина запаса будет различной в каждую единицу времени, то и расходы по хранению будут различны. Проведем в D0AD1 среднюю линию AC и опустим перпендикуляр CE.В силу равенства треугольников DABC и DECD1 величина запаса в любой точке левее точки E больше величины 0A= y/2 настолько, насколько меньше этой величины в точке, симметричной относительно E. Поэтому на всем отрезке [0; D1] можно считать, что в среднем хранится величина y/2. Таким образом, для величины средних затрат в единицу времени получаем следующее выражение:

S₁(y)= c₁β + Kb/y + hy/2, (3)

если y<q и

S₂(y)= c₂β + Kb/y + hy/2 (4)

в противном случае.

Здесь первое слагаемое выражает затраты на закупку товара, продаваемого магазином в единицу времени. Второе ― затраты на оформление заказа, отнесенные к единице времени. Третье ― средние затраты на хранение запаса в единицу времени. Так как первое слагаемое в зависимости от y меняется один раз на постоянную величину, то минимум у этих функций достигается в одной точке.

Найдем минимум этого выражения по величине заказа y. Для этого вычислим производную и приравняем ее нулю.

- Kb/y² + h/2 = 0. i= 1,2 (5)

Из равенства (5) получаем формулу экономичного размера заказа Уилсона

y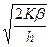^*= . (6)

Если бы цена на товар была постоянной (не зависела от объема закупаемой партии), то величина y^* была бы оптимальной. Действительно, вторая производная функции S_i(y) больше нуля в области y> 0. Следовательно, функция S_i(y) выпуклая в этой области, а точка y^* доставляет минимум этой функции.

В случае разрыва цен величина оптимальной партии y_opt зависит от величины q.

S ₁(q)

Если y^* ³ q, тогда y_opt = y^*. Так как в этом случае при закупке партии в объеме y^* будет получена скидка и суммарные затраты в единицу времени составят наименьшую из всех величину S₂(y^*). Пусть y^* < q, тогда y_opt = q, если q £ y₁. Здесь y₁ ¾ больший корень уравнения

S₁(y^*) = S₂(y). (7)

Если же q > y₁, то y_opt = y^*. Таким образом, если q £ y₁, то выгодно воспользоваться скидкой, в противном случае ¾ нет (рис. 2).

Пусть оптимальный объем заказываемой партии определен и равен y_opt. Точка заказа R определяется из соотношений

R = b´t^*, t^* < t;

R = b´(t^*-m´t),

где m ¾ целая часть от деления t^* на t, а t = y_opt /b, так на рис.1 величина t^* равна длине отрезка [ G; D ₃]. При этом m =2, а величина R показана на оси y.

Пример 1. Магазин закупает товар для продажи. Ежедневный спрос на товар в магазине ¾ 30 ед., стоимость хранения одной единицы товара на складе составляет 0,15 денежных единиц (д.ед.), стоимость оформления заказа ¾ 100д.ед. Цена одной единицы товара 10 д.ед., если объем закупаемой партии меньше 300 ед. и 8 д.ед. в противном случае. Определить объем закупаемой партии и точку заказа, если время выполнения заказа ¾ 12 суток.

Решение. Найдем y^*. По формуле (6) получаем

y^* = .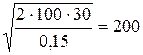

Так как y^* меньше объема q= 300, за который дают скидку, то нужно сравнить q и y₁. Найдем y₁, решая уравнение (7).

.

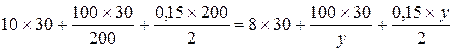Приводим к общему знаменателю и решаем квадратное уравнение

.

Наибольший корень этого уравнения равен

y₁ = + .

Так как y₁ > q, то y_opt = q =300, следовательно,

t= y_opt /b =300/30 = 10.

Для нахождения точки заказа найдем число m = . Тогда

R= 30(12-1´10)=60.

Ответ. Необходимо заказывать 300 ед. товара, когда на складе останется 60 ед. товара.

Дата добавления: 2015-05-08