Однопродуктовая n - этапная динамическая модель без дефицита

В данной модели предполагается, что уровень запаса контролируется периодически, а запаздывание с поставкой товара либо равно нулю, либо кратно периоду контроля. Поэтому будем считать, что пополнение запаса происходит мгновенно в начале этапа. Спрос также удовлетворяется мгновенно в начале этапа. Дефицит не допускается. Рассматривается конечный горизонт (n этапов) планирования. Отметим, что параметры этой модели меняются от этапа к этапу, то есть зависят от времени. Время меняется дискретно на величину этапа.

Обозначим:

y _i - количество заказываемой продукции на i –м этапе;

b _i- спрос на продукцию на i –м этапе;

x _i- запас продукции на начало i –го этапа;

h _i- затраты на хранение единицы продукции, переходящей с этапа i на этап i +1;

K _i- затраты на оформление заказа на i –м этапе;

c _i(y) - затраты на закупку продукции на i –м этапе при условии, что объем закупаемой партии равен y.

Требуется найти значения 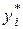на всех этапах i= 1,…, n, минимизирующие суммарные затраты по всем этапам.

Обозначим C_i(y) все затраты на закупку продукции объемом y на этапе i, тогда

.

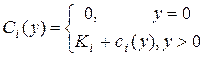Для дальнейшего рассмотрения удобно представлять процесс поступления на склад и расходования со склада продукции в виде схемы:

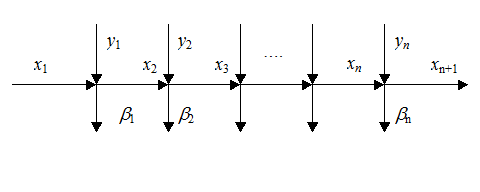
Для решения задачи будет применяться метод динамического программирования. Этот метод позволяет разбить исходную задачу поиска оптимума на всем горизонте планирования на n подзадач поиска экстремума на каждом этапе. Пусть состоянием системы на i –м этапе будет объем запаса x _i+1. Так как планируется минимизация затрат только на этапах от 1 до n, то величина x _n+1 должна быть равна нулю. В этом случае объем запаса x _i не должен превышать величину суммарного спроса на этапах i,…, n,

(31)

Пусть f_i(x_i+1) - минимальные суммарные затраты на этапах 1,…, i при заданной величине запаса x_i+1 на конец этапа i. Тогда рекуррентное уравнение будет иметь вид

;

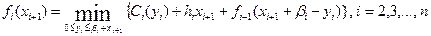
Таким образом, на первом этапе по заданному запасу x ₂ величина y ₁ определяется однозначно. На последующих этапах величина y _i определяется из условия минимума суммарных затрат на этапе i (первые два слагаемых) и на всех предыдущих этапах 1,…, i- 1 (третье слагаемое). Аргумент функции f_i-1(x_i) вычислен из соотношения

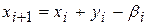. (32)

Следуя методу динамического программирования, последовательно находятся значения функций f ₁, f ₂,, f _n. Это прямая прогонка. Затем, начиная с номера n и до номера 1, вычисляются оптимальные значения 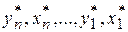- обратная прогонка.

Пример. Рассмотрим 3 – этапную систему управления запасами. Пусть начальный запас равен 1 единице продукции. Стоимость закупки единицы продукции составляет 10 д. ед. за каждую из первых трех единиц продукции и 20 - за каждую единицу продукции сверх 3. Остальные данные представлены в таблице

i	b I	K i	h i

В рассматриваемой задаче затраты на закупку можно записать следующим образом:

Вычисление функций 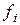, i = 1,…, n производится по этапам.

Этап 1. Вычисление значений функции сведем в таблицу

x 2	h 1 x 2	y 1	C 1(y 1)

Здесь интервал изменения x ₂ вычислен по формуле (31):

0 £ x ₂ £ b ₂ + b ₃ =2 + 4 = 6,

а величина y ₁ для каждого x ₂ находится из соотношения (32):

y ₁ = x ₂ - x ₁ + b ₁.

Этап 2. Интервал изменения x ₃ будет от 0 до 4. Вычисление значений функции f ₂(x ₃) приведено в следующей таблице

x 3	h 2 x 3	y 2=0							f 2(x 3)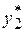
C 2=0
					-	-	-	-
						-	-	-
							-	-
								-

Для каждого значения x ₃ (соответствующая строка) и каждого значения y ₂ (соответствующий столбец) в ячейке таблицы находится значение выражения

, (33)

где в силу (32) x ₂ = x ₃ - y ₂ + b ₂.Величина y ₂ изменяется в интервале

0£ y ₂ £ x ₃ - x ₂ + b ₂.

При этом максимальное значение y ₂ будет достигаться при максимальном значении x ₃ и минимальном значении x ₂. Следовательно,

0£ y ₂ £6.

Отметим, что этот интервал совпадает с интервалом изменения x ₂. Покажем нахождение этих значений для двух случаев x ₃ =0 и x ₃ =1. Для x ₃ =0 получаем

=0+0+55,

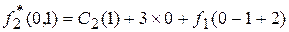=17+0+34=51,

=27+0+23=50.

Вычисление для y ₂ >2 невозможно, так как значение аргумента функции f ₁ будет отрицательным, что недопустимо по условиям задачи. Поэтому в соответствующих ячейках стоит прочерк. Минимальное значение по строке 50 равно значению функции f ₂(0) и расположено в столбце f ₂(x ₃) таблицы. В столбце 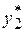этой таблицы расположено значение y ₂, при котором достигается это минимальное значение (в рассматриваемом случае это y ₂ =2). Для x ₃ = 1 будем иметь

0+3+76=79;

17+3+55=75;

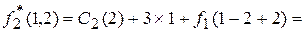27+3+34=64;

37+3+23=63.

Вычисление 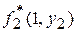для y ₂ >3 невозможно по причине, аналогичной предыдущей. Минимальное значение по строке 63 равно значению функции f ₂(1) и расположено в столбце f ₂(x ₃) таблицы. В столбце 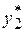этой таблицы расположено значение y ₂, при котором достигается это минимальное значение (в рассматриваемом случае это y ₂ =3).

Этап 3. Переменная x ₄ может принимать единственное значение, равное нулю, y ₃ изменяется в пределах от 0 до 4. Соответствующие значения и f ₃(0) приведены в следующей таблице:

x 4	h 3 x 4	y 3=0	y 3=1	y 3=2	y 3=3	y 3=4	f 3(x 3)
C 3=0	C 3=16	C 3=26	C 3=36	C 3=56

В соответствии с полученным результатом минимальные суммарные затраты равны 99. Теперь нужно найти величины . Будем находить их, двигаясь по таблицам в обратном направлении. Величину = 3 получим из последней таблицы. Найдем из соотношения (32)

= x ₄ - + b ₃=0 - 3 + 4=1.

Теперь из предпоследней таблицы в строке = 1 находим = 3. Соответственно,

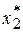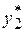= - + b ₂=1 - 3 + 2 = 0.

Из первой таблицы в строке 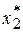= 0 находим = 2.

Ответ. Для минимизации суммарных затрат необходимо на первом этапе заказать 2 единицы продукции, на втором - 3 единицы, а на третьем также 3 единицы. Суммарные затраты составят 99 д. ед.

Дата добавления: 2015-05-08