Однопродуктовая статическая модель при допущении дефицита

В отличие от предыдущего пункта в данной модели предполагается, что цена на товар - величина постоянная. Допускается дефицит. Как и ранее товар поставляется партиями через некоторые промежутки времени t. Интервал [0;C] длиной t делится на два (рис.3). В течение первого интервала [0;A) длительностью t₁ непрерывный спрос интенсивностью b удовлетворяется из запаса, имеющегося на складе. В течение второго интервала [A;C] длительностью t₂ спрос не удовлетворяется. Накопленный неудовлетворенный спрос покрывается немедленно при поступлении следующей партии товара. За несвоевременную поставку товара взимается штраф.

Штраф может толковаться и как штрафные санкции, и как упущенная прибыль. Будем предполагать, что взимается p денежных единиц за единицу недопоставленного товара в течение единицы времени.

y

B

0 А С

D E

	Рис. 3

Обозначим: y - объем заказываемой партии (длина отрезка [D;B]); q - максимальное количество товара на складе (длина отрезка [0;B]). В рассматриваемой задаче нужно выбрать два параметра: y и q. Цель – минимизация суммарных затрат в единицу времени.

Как и в предыдущем случае, можно найти суммарные затраты на периоде от момента поставки товара до следующего момента поставки. Затем разделить их на длину периода и получить суммарные затраты в единицу времени. Далее, как и предыдущей задаче, будем обозначать:

K - стоимость оформления заказа;

h - стоимость хранения единицы товара в единицу времени;

H - суммарные затраты на периоде между поставками (например [0;C]);

t^* - время выполнения заказа;

t - длина интервала [0, C] между поставками;

t₁ - длина интервала [0, A];

t₂ - длина интервала [A, C].

Выразим величины t₁ и t₂ через величину t. Из подобия треугольников DDBE, D0BC и DACE получаем:

.

Следовательно,

; (8)

На рассматриваемом интервале [0, C] только в течение интервала [0, A] на складе имеется запас товара и, следовательно, затраты по хранению товара. Аналогично, только на интервале [A, C] имеется дефицит и затраты, связанные с ним. Как и в предыдущей задаче, средний уровень запаса на складе на интервале [0, A] равен q/2. Средний уровень дефицита в течение интервала [A, C] равен (y-q)/2. Тогда затраты на хранение и потери от дефицита на отрезке [0, C] будут, соответственно, следующие:

, .

Суммарные затраты на отрезке [0, C] будут состоять из этих затрат и затрат на оформление заказа. Заменяя t₁ и t₂ из соотношения (8), получим

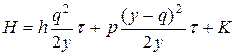. (9)

Найдем суммарные затраты в единицу времени, разделив величину H на длину рассматриваемого интервала t (как и в предыдущей задаче t = y/b).

. (10)

Запишем необходимое условие минимума.

;

.

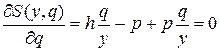Разрешая данные уравнения относительно y и q, получаем:

; . (11)

При этом длина периода и минимальные суммарные затраты будут задаваться соотношениями

; . (12)

Отметим, что при этом ,

т.е. отношение стоимостей хранения и стоимости дефицита единицы товара в единицу времени обратно пропорционально отношению максимального объема запаса и максимального объема дефицита.

Найдем теперь точку заказа R. В отличие от предыдущей модели в момент заказа на складе может либо быть некоторое количество товара, либо накоплен некоторый объем дефицита. Поэтому под точкой заказа будем понимать объем либо товара, либо дефицита, при котором нужно делать новый заказ. Так же, как и в модели без дефицита, нужно для оптимального объема заказа y^* определить величину t^* (12). Затем найти число m,равное целой части от деления t^* на t^*и число t_* = t^* - m´ t^*. Тогда точку заказа можно найти из соотношения

(13)

Первая строчка соответствует точке заказа, равной объему товара, при котором нужно делать новый заказ, а вторая - объему дефицита.

Пример 2. Мелкооптовый магазин закупает товар партиями для реализации. Спрос на товар составляет 10ед. в день. Если товара нет на складе, то он поставляется позже при закупке магазином следующей партии. За несвоевременную поставку товара магазин выплачивает штраф в размере 0,6 д. ед. за просрочку поставки единицы товара на одну единицу времени. Стоимость хранения единицы товара на складе магазина в течение единицы времени составляет 0,3 д. ед Стоимость оформления заказа составляет 9 д. ед Время поставки товара в магазин - 5 дней. Требуется определить объем закупаемой магазином партии товара, максимальный объем товара на складе и точку заказа с тем, чтобы суммарные затраты в единицу времени были минимальны.

Решение. В соответствии с условиями задачи имеем:

K= 9; b= 10; p= 0,6; h= 0,3.

По формулам (11) находим оптимальный объем заказываемой магазином партии и максимальный объем товара на складе

, .

По формуле (13) найдем длину периода t^*, а по формуле (8) длину интервала времени, при котором имеется дефицит t₂.

; .

Теперь определим числа m и t_*

m= [5/3]=[1.67]=1, t_* = t^* - m´ t^* =5 -1´3=2.

Так как t_* > t₂, то точка заказа будет считаться по верхней строчке формулы (13):

R= (t_* -- t₂) b = (2 -1)´10=10.

Таким образом, с целью минимизации средних суммарных затрат в день необходимо заказывать 30 единиц товара, когда на складе осталось 10 единиц. При этом максимальная величина продукции на складе составит 20 единиц.

Дата добавления: 2015-05-08