Контрольна робота №18

1. Забезпечення плавності дороги введенням перехідних кривих-клотоїд.

Найбільша плавність траси дороги забезпечується введенням довгих перехідних кривих, описаних по клотоїді з рівнянням в параметричному вигляді А2 = RL. Значення параметра А перехідних кривих повинно знаходитися в межах від 0,4r до 1,4r, причому параметри суміжних кривих не повинні розрізнятися більш ніж в 1,5 рази.

Для зорової плавності дороги кут повороту траси при вписуванні перехідних кривих повинен складати не менше 3°. Довжина кожної перехідної кривої має бути не менше 1/4 довжини кругової кривої. При сполученні перехідними кривими зворотних s-образних кривих бажано, щоб обидві перехідні криві мали однакові значення параметрів А. При цьому радіуси кривих, що сполучалися, повинні знаходитися в співвідношенні R1 £ 3R2.

При сполученні перехідними кривими кругових кривих одного знаку слід дотримувати співвідношення

0,5 R ₁ < A < R ₂;

А ₁ £ А ₂ £ 1,2 А.

При R ₁ £ 2 R ₂ кругові криві можна сполучати між собою безпосередньо. Довжина прямої вставки між зворотними клотоїдами з параметрами А1 і А2 не повинна перевищувати

L = (А ₁ + А ₂)/2.

При цьому параметри А1 і А2 не повинні розрізнятися більш ніж в два рази.

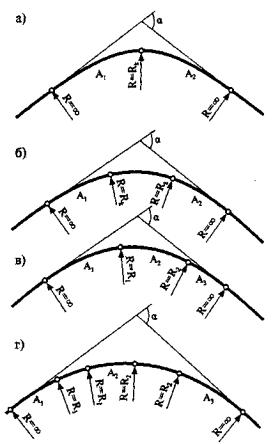
Рис. 1. Типи заокруглень клотоїдної траси

2.Основні прийоми трасування в гірській місцевості.

У гірській місцевості висотні елементи ландшафту переважають настільки, що будь-яка непокора їм дороги зв'язана з різким збільшенням кошторисної вартості будівництва. Узгодження з ландшафтом для гірських доріг зводиться до огинання елементів гірського рельєфу з відхиленням від них на мінімальні відстані, необхідні для дотримання вимог до елементів плану і поздовжнього профілю в складних умовах рельєфу.

При забезпеченні досить високих технічних нормативів для автомагістралей геометрична правильність їхнього контура набуває вирішальної ролі у формуванні нового ландшафту гірської місцевості. Дорога стає пануючим і організуючим елементом крутих схилів гірського ландшафту, не зачепленого діяльністю людей. правильними елементами дороги і хаотичністю гірського ландшафту. Монументальні інженерні споруди - серпантини, підпірні стінки, мости, балкони, тунелі, протилавинні і протиселеві галереї, виділяючись на одноманітній поверхні гірських схилів, зосереджують увагу і визначають характер ландшафту. В даному випадку гармонійне поєднання дороги з ландшафтом досягається контрастністю між геометрично правильними елементами дороги і хаотичністю гірського ландшафту.

У узгодженні доріг з ландшафтом в гірській і сильно пересіченої місцевості істотного значення набуває оформлення укосів і оголень схилів що утворюються при влаштуванні земляного полотна на полицях узгір'їв. Засобом маскування оголень можуть бути посадки чагарника і повзучих рослин в грунт, якими заповнюють видовбані в укосі кишені.

Дата добавления: 2015-05-07