Скалярные и векторные поля в гидроаэромеханике

При изучении движения жидкости рассматривают ее как сплошную среду. Таким, образом рассматривают не движение конечного числа отдельных частиц, а поля различных физических величин: скорости, плотности, давления и т. д. Математически эти поля описываются системой функций от координат и вре­мени.

Такой подход типичен не только для механики сплошных сред (аэродина­мики, теории упругости, реологии и т. д.), но и для ряда других областей фи­зики.

В общем случае поле является пространственным (трехмерным), однако иногда можно упростить задачу и изучать одномерные или плоские двумерные поля. В этом случае предполагают, что физические величины зависят соответ­ственно только от одной или двух пространственных координат.

Если физические величины не зависят от времени, то поле называется ста­ционарным, в противоположном случае — нестационарным.

При математическом описании полей предполагают, что существуют пре­делы значений физических величин в точке. Так, например, плотность жидкости в точке определяется как предел отношения массы жидкости, заключенной в не­котором объеме, к этому объему, когда он стремится к нулю. Такой подход при­водит к упрощению физической реальности, так как не учитывает дискретности строения материи. Очевидно, что такая абстракция вполне оправдана и нужно только разумно ограничить область применения полученных результатов.

Так, основываясь на предыдущем примере, следует принять, что объем, в ко­тором вычисляется средняя плотность жидкости, значительно больше молеку­лярных размеров, но в то же время значительно меньше некоторой характерной длины, на которой происходит заметное изменение плотности. Так как в пода­вляющем числе практических задач размеры обтекаемых тел, длины звуковых волн и т. п. на много порядков больше молекулярных размеров, то в этих зада­чах жидкость можно рассматривать, как сплошную среду.

Опишем кратко характеристики полей, которые встречаются в гидроаэро­механике.

Скалярным называется поле, которое характеризуется в каждой точке про­странства одним числом. Такое поле описывается одной функцией, зависящей от трех координат. Скалярным будет, например, поле плотности или темпера­туры.

Вместо обычного обозначения декартовых координат xyz удобно принять обозначения x₁x₂x₃. Это позволит ввести индексные обозначения, что в дальней­шем сократит и упростит все преобразования.

Основное свойство скалярной функции a (х₁, х₂, x₃) состоит в том, что ее чис­ленное значение не изменяется при преобразовании координат. Если перейти от старой х₁х₂х₃ к новой х'₁х'₂х'₃ системе координат, то значения плотности или температуры в фиксированной точке пространства, естественно, не изме­нятся a(x`<sub>1</sub>,x`₂,x`₃) = a(x₁,x₂,x₃)

Векторным называется поле, которое характеризуется в каждой точке про­странства величиной и направлением. Векторным будет, например, поле скоро­стей жидкости. Вектор а (в пространстве трех измерений), как известно, может быть задан тремя компонентами v₁(x1,x2,x3), v₂(x1,x2,x3), v₃(x1,x2,x3).

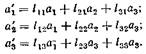
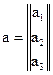Это можно записать также в виде таблицы из трех величин? т.е. тремя функциями от трех переменных или, более кратко, одной величиной с индексом: a = a_i, который принимает значе­ние i = 1, 2, 3. При такой записи предполагается, что а_i — это i-я компонента вектора а. В даль­нейшем применяется эта индексная запись.

Введем новую декартову систему координат x'₁, x'₂, x'₃ с тем же началом, но другим направлением осей. Обозначим через l_ij. направляющий косинус оси x '_j, относительно оси x_i (i = 1, 2, 3; j = 1, 2, 3). Вычислим проекции того же век­тора, а на новые оси координат

Следовательно, вектор подчиняется определенному закону преобразования его компонент (5) и отличается от скалярной величины, численное значение которой не меняется при преобразовании координат. Очевидно, что сам вектор не меняется в новых координатах, а меняются только его компоненты.

Целесообразно принять индексную форму записи, основанную на общепри­нятых соглашениях.

Выражения (1.5) можно представить в виде суммы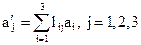

В дальнейшем, как это принято, будем применять еще более короткую запись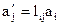

При такой записи пользуются двумя правилами.

1. Соглашение о суммировании. По индексу, встречающемуся дважды (не­мой индекс), производится суммирование от 1 до 3.

2. 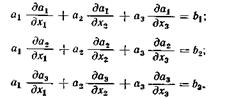Соглашение о ранге. Индекс, встречающийся один раз (свободный ин­декс), пробегает значения от 1 до 3. Таким образом, уравнение с одним свобод­ным индексом означает запись трех уравнений.

Соглашения о суммировании и ранге относятся не только к векторам, а вообще к любой записи и любым операциям (если нет специальной оговорки о против­ном).

Так, например, краткая запись 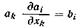означает (здесь индекс k — немой, индекс i — свободный)

Отметим, что немой индекс при суммировании заменяется цифрами, по­этому немой индекс пропадает и его можно заменить любой буквой. Можно, например, заменить индекс k на п, но не i, так как i в данном случае принят в качестве свободного индекса.

Приведем другой пример (индекс i - немой, свободного индекса нет) u_iu_i = и²₁ + и²₂ + u²₃.

Отметим также, что все члены должны иметь один и тот же свободный ин­декс (или вообще не иметь свободного индекса). Это означает, что все члены урав­нения представляют проекцию на одну и ту же ось координат.

Приведем в качестве примера, на который будем ссылаться в дальнейшем индексную запись скалярного произведения векторов.

Пусть имеются два вектора а и b, которые можно задать их компонен­тами а_i и b_i. Как известно, скалярное произведение двух векторов можно выразить через сумму произведений компонентов а*b = a₁b_l+a₂b₂+a₃b₃. Следовательно, в индексной записи скалярное произведение выглядит так: а*b = a_ib_i (7)

Дата добавления: 2015-05-09