Уравнение переноса

Движущаяся жидкость может переносить не только массу, количество дви­жения, энергию, что рассматривалось при выводе основных уравнений сохра­нения, но также иные вещества и свойства. Так, в общем случае жидкость может переносить примеси: мелкие твердые частицы, капли другой жидкости и т. п. или какие-нибудь свойства и качества: завихренность, энтропию и т. д.

Положим, что жидкость переносит какую-нибудь материальную среду или свойство, подчиняющееся закону сохранения. Обозначим содержание перено­симого вещества или свойства в единице объема жидкости h. Тогда по полной аналогии с изложенным в разд. 2.1 можем записать уравнение переноса в инте­гральной форме 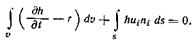(2.34)

Здесь rможно назвать источником величины h внутри выделенного объема. Сле­довательно, rпоказывает, какое количество h возникает внутри единицы объема жидкости в единицу времени.

Уравнение (2.34) может быть записано в дифференциальной форме (также по аналогии с предыдущими выводами) 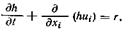(2.35)

В данном случае рассматривается перенос какой-либо среды или свойства благодаря движению жидкости. Если скорость жидкости равна нулю, a источ­ники переносимого вещества отсутствуют, то, как следует из уравнения (2.31) 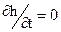. Следовательно, концентрация вещества не меняется в данной точке со временем. Значит, в данном конкретном случае не рассматривается перенос путем диффузии, который происходит и в покоящейся жидкости, если концентрация вещества распределена неоднородно по объему. Для примера достаточно вспомнить рассеивание дыма, т.е. диффузию мельчайших твердых частиц.

Учесть рассеивание переносимого вещества вследствие диффузии можно так же, как это было сделано в разд. 2.3 при подсчете теплоты, переданной объ­ему благодаря теплопроводности (диффузии молекул). Тогда вместо (2.35) получим уравнение 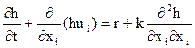(2.36),

здесь k – коэффициент диффузии.

2.5. ПРИМЕНЕНИЕ УРАВНЕНИЙ СОХРАНЕНИЯ В ИНТЕГРАЛЬНОЙ ФОРМЕ

Некоторые задачи могут быть просто решены применением уравнений со­хранения, записанных в интегральной форме. Наиболее просто решаются за­дачи для установившегося течения, так как в этом случае необходимы данные о потоке только на поверхностях, ограничивающих область течения, и нет необ­ходимости рассматривать особенности течения внутри области. Таким образом могут быть получены только суммарные характеристики потока. Важно также отметить, что уравнения в интегральной форме пригодны для расчета потоков с разрывами, т. е. скачкообразными изменениями параметров.

Приведем несколько примеров применения уравнений сохранения в инте­гральной форме, на которых можно глубже разобраться в существе самих урав­нений и методике их использования. Полученные результаты представляют также· самостоятельный интерес, так как используются в технических расчетах.

1. Установившееся одномерное течение идеальной несжимаемой жидкости в поле тяжести. Пусть площадь трубы изменяется столь плавно, что в каждом поперечном сечении скорость постоянна по сечению и перпендикулярна ему (одномерность течения). Найдем запись уравнения энергии для данного случая.

Рассмотрим сначала уравнение неразрывности в интегральной форме (2.5). Первый интеграл равен нулю, так как плотность не изменяется, а источников массы внутри трубы нет. Второй интеграл следует взять по площади, ограничи­вающей выделенный объем жидкости. Объем жидкости ограничен стенками трубы и двумя произвольно выбранными поперечными сечениями F_l и F₂. Инте­грал, вычисленный по поверхности стенок, равен нулю, так как равна нулю нормальная к ним проекция скорости (стенки непроницаемы). Скорость нор­мальна к поперечным сечениям и поэтому получим

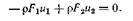(2.37)

Перед первым членом поставлен знак минус, так как жидкость втекает в объем. Уравнение выражает тот факт, что расход массы через каждое поперечное сечение, постоянен. В данном случае плотность жидкости постоянна и поэтому постоянен объемный расход.

Используем уравнение энергии в интегральной форме (2.27). Первый инте­грал равен нулю, так как течение установившееся. Пятый и шестой интегралы равны нулю, так как подвода теплоты и теплообмена нет. Во втором интеграле можно опустить член, учитывающий внутреннюю энергию, так как температура жидкости не меняется. При вычислении второго интеграла интегрирование про­водится только по площади поперечных сечений, так как проекция скорости на нормаль к стенке трубы равна нулю. Следовательно, получим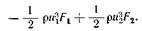

Третий интеграл вычисляется по объему жидкости, заключенному между вы­бранными поперечными сечениями. Запишем следующие выражения: dv = Fds, u_if_i = ug cos(α), где ds — элемент длины вдоль оси трубы; a — угол между касательной к оси трубы в данной точке и направлением действия силы тяжести. Сила, действующая на единицу массы жидкости, в данном случае равна ускорению силы тяжести, и третий интеграл вычисляется также просто 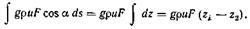(2.38)

Произведение ruF вынесено за знак интеграла, так как оно постоянно для любого сечения в силу уравнения неразрывности (2.37). Координата z измеряется в направлении действия силы тяжести.

В четвертый интеграл уравнения (2.27) входят напряжения, действующие по поверхности выделенного объема. Поскольку в идеальной жидкости силы трения равны нулю, то напряжения равны силам давления, действующим по нормали к поверхности. На стенках трубы нормальная проекция скорости равна нулю, и поэтому интеграл вычисляется только по выбранным поперечным сечениям, т. е. равен u₁p₁F₁ – u₂p₂F₂.

Силы давления на контрольных поверхностях направлены внутрь выделен­ного объема. Перед вторым членом поставлен знак минус, так как направление силы противоположно направлению скорости. После преобразований получим так называемое уравнение Бернулли

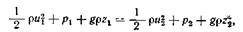(2.39)

которое является одним из основных уравнений механики несжимаемой жид­кости. Уравнение Бернулли является, как будет показано далее, интегралом уравнения движения и совпадает с уравнением энергии только в частном случае. Каждый член уравнения Бернулли выражает энергию единицы массы жидкости. Первый член соответствует кинетической энергии, второй представ­ляет работу сил давления, а третий — потенциальную энергию силы тяжести.

2. Уравнение Бернулли для потока в системе вращающейся с постоянной угловой частотой. Пусть ось трубы переменного сечения лежит в плоскости, проходящей через ось вращения. Труба, по которой течет несжимаемая идеаль­ная жидкость, вращается с постоянной угловой частотой.

Рассматриваем течение в относительном движении, т. е. в системе коорди­нат, связанной с вращающейся трубой. Уравнения механики справедливы и во вращающихся системах, если в дополнение к действующим в абсолютной си­стеме силам добавить две массовые силы (силы инерции), соответствующие цен­тростремительному и кориолисову ускорениям, взятым с обратным знаком. Кориолисово ускорение направлено по нормали к относительной скорости жид­кости, и поэтому при вычислении третьего интеграла в уравнении (2.27) даст результат, равный нулю. Тогда вывод уравнения не отличается от предыдущего вывода и только при вычислении третьего интеграла в уравнении (2.27) надо подставить центростремительное ускорение, взятое с обратным знаком.

Интеграл по объему вычисляется по аналогии с проделанным ранее вычис­лением (2.38):

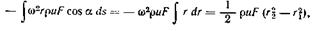
где ω — частота вращения; r — текущий радиус вращения; α — угол между касательной к оси трубы в данной точке и радиусом.

Тогда окончательное уравнение записывается в таком виде (член, учитываю­щий силу тяжести, в данном случае не записываем) 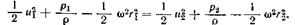(2.40)

Это уравнение применяется, например, при расчете центробежных насосов.

Дата добавления: 2015-05-09