Уравнение неразрывности. Основные уравнения гидроаэромеханики основываются на законах сохранения массы, количества движения и энергии

Основные уравнения гидроаэромеханики основываются на законах сохранения массы, количества движения и энергии, кото­рые вместе обычно кратко именуются законами сохранения. Особенность заключается в том, что в механике жидкости эти законы необходимо записать в форме, пригодной для изучения движения сплошной деформируемой среды.

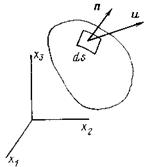
Уравнением неразрывности называют закон сохранения массы. Рассмотрим в потоке жидкости некоторую произвольную фикси­рованную замкнутую поверхность s, ограничивающую объем ν. Выделим на поверхности элемент площади d s и построим единич­ный вектор n, направленный наружу по нормали к поверхности (рис. 2.1). Поток жидкости пронизывает замкнутую поверхность, причем через выделенный элемент поверхности за единицу вре­мени протекает масса жидкости, равная pu,ds, где и_п — нормаль­ная к поверхности составляющая скорости жидкости; ρ - плот­ность жидкости. Проекцию скорости на нормаль можно заменить через скалярное произведение вектора скорости и на единичную нормаль n: pnuds. В индексной записи [см. формулу (1.7) ] это вы­ражение примет вид ρη_iu_ids.

Интегрируя по поверхности, получим массу, вытекающую за единицу времени из фиксированного объема: 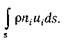(2.1)

Пусть в общем случае в жидкости распределены источники массы, которые подают на единицу объема в единицу времени массу т. Тогда внутрь фиксированного объема за единицу времени поступает масса, равная 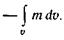(2.2) Знак минус учитывает, что в выражении (2.1) было принято, что вытекшая масса берется со знаком плюс.

Масса жидкости, заключенная внутри выделенного объема, за единицу времени изменится, как следует из выражений (2.1) и (2.2), на величину 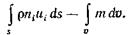(2.3)

Масса в фиксированном объеме может изменяться только в том случае, если изменяется во времени плотность жид­кости.

Скорость изменения массы, заключенной в объеме, можно представить следующим образом:

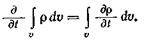(2.4)

Здесь переход к дифференцированию под знаком интеграла воз­можен, так как объем постоянен.

Из выражений (2.3) и (2.4) можно записать закон сохранения массы в интегральной форме

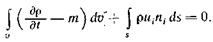(2.5)

Для того чтобы получить это уравнение в дифференциальной форме, воспользуемся формулой Гаусса – Остроградского, кото­рая позволяет преобразовать интеграл по поверхности в интеграл по объему, ограниченному этой поверхностью: 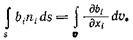(2.6)

Здесь величина b_i имеет один индекс, т. е. является вектором. Аналогичная формула справедлива, если b является скаляром (т. е. не имеет индексов) или тензором (имеет два индекса)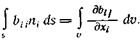

(2.7)

Положив в формуле (2.6) b_i – равным ru_i, заменим в выражении (2.5) интеграл по поверхности интегралом по объему и получим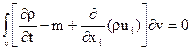

Полученное уравнение справедливо для произвольного объема, но тогда интеграл может быть равен нулю, только если равно нулю подынтегральное выражение. Отсюда следует уравнение неразрывности в дифференциальной форме 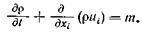(2.8)

Запишем это уравнение для отдельных частных случаев. Если источников массы нет, тогда 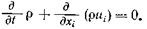(2.9)

Если рассматриваем стационарное движение сжимаемой жидко­сти, 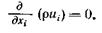(2.10)

то dr/dt = 0 и, следовательно,

Если жидкость несжимаема, то уравнение неразрывности при­нимает 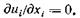(2.11)

наиболее простую форму

Дата добавления: 2015-05-09