Поверхностные силы

Помимо скалярных и векторных полей в механике сплошной среды рассматриваются еще тензорные поля.

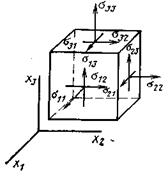
Вырежем в жидкости элементарный параллелепипед с ребрами dx₁ dx₂ и dx₃ (рис. 1.1). На грани этого параллелепипеда со сто­роны остальной жидкости действуют поверхностные напряжения. В общем случае на каждую грань действуют как нормальные, так и касательные напряжения. В принятой записи (см. рис. 1.1) каждое из напряжений σ_ijимеет два индекса. Первый индекс озна­чает ориентацию площадки, на которую действует напряжение, второй — ось проектирования. Так, например, σ₂₁ — это напря­жение, которое действует на площадку, перпендикулярную оси х₂ и параллельно оси х1.

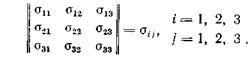
Компоненты напряжений можно записать в виде таблицы (Матрицы тензора напряжений) или коротко одной буквой с двумя индексами (8)

Здесь первый номер означает номер строки, второй — номер столбца. Нор­мальные напряжения имеют два одина­ковых индекса (диагональ матрицы), касательные напряжения имеют разные индексы. Такой тензор называют тензо­ром второго ранга (по числу индексов у компонент).

Тензор более общее понятие, чем вектор или скаляр. Компоненты вектора имеют один индекс (4) и он может быть записан матрицей (таблицей) из одного столбца (3). Вектор называют тензором первого ранга.

Скаляр, представляемый буквой без индекса (1), называют тензором нулевого ранга.

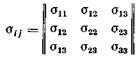Тензор второго ранга в общем случае описывается девятью функциями трех переменных. Однако тензор напряжений (8) обладает одной важной особенностью. Из условия равенства нулю моментов, действующих на элементарный объем (см. рис. 1.1), следует, что касательные напряжения с одинаковыми, но рас­положенными в обратном порядке индексами равны σ_ij = σ_ji. Такой тензор называется симметричным и вместо (8) можно написать (9)

Значит, тензор напряжений выражается через шесть функций трех переменных.

Компоненты напряжений представляют как нормальные (σ₁₁, σ₂₂, σ₃₃), так и касательные (σ₁₂, σ₁₃, σ₂₃) напряжения. Касательные напряжения возникают вследствие вязкости, которой обладают все реальные жидкости. Однако вязкость и, следовательно, каса­тельные напряжения проявляются только при движении жидкости. В покоящейся вязкой жидкости касательные напря­жения отсутствуют (так как скорости деформаций равны нулю), а нормальные напряжения создаются давлением и не зависят от ориентации площадки (закон Паскаля).

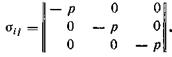Напомним, что в гидроаэромеханике вводится понятие идеаль­ной жидкости, как жидкости, полностью лишенной вязкости. Следовательно, в идеальной жидкости касательные напряжения отсутствуют и при движении, а тензор напряжений принимает вид (10)

Перед давлением p по условию поставлен знак минус, так как давление обычно сжимает жидкость, т. е. действует против поло­жительного направления нормали к площадке.

Таблицу (10) можно сокращенно записать в виде 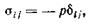(11)

где вводится символ, определяемый условиями 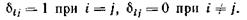(12)

При рассмотрении движения вязкой жидкости также целесооб­разно выделить ту часть нормального напряжения, которая не зависит от вязкости, и записать тензор напряжений (1.9) в таком виде

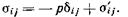(13)

Здесь напряжения σ`_ij зависят от вязкости. Если i ¹ j, то второй член справа представляет касательные напряжения. Если i = j, то этот член выражает добавочные нормальные напряжения, вызванные вязкостью жидкости. Эти добавочные нормальные напряжения весьма малы по сравнению с давлением.

Величины σ_ij представляют напряжения по трем взаимно пер­пендикулярным граням. Однако необходимо также знать напря­жения, которые действуют на произвольно ориентированную грань. Их можно выразить через напряжения σ_ij.

Рассмотрим элементарный тетраэдр (рис. 1.2), к которому приложены только поверхностные силы. Напряжения на трех взаимно перпендикулярных гранях задаются тензором σ_ij. Ориен­тация косой площадки определяется вектором единичной нор­мали n.

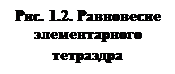Компоненты напряжений на косой площадке находятся из условий равновесия элементарного тетраэдра (формула Коши)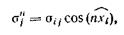

где согласно принятому ранее обозначению σⁿ_j — проекция на ось х_j напряжения на площадке, ориентация которой задана нормалью n; 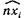— угол между нормалью и осью x_i.

Поскольку вектор n имеет длину, равную единице, то его компоненты по осям координат равны направляющим косинусам: 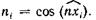Следовательно, предыдущая формула примет вид 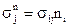(14)

Таким образом, зная тензор напряжений σ_ij, можно вычислить компоненты напряжений на произвольно ориентированной пло­щадке.

Повернув оси координат, можно показать, что компоненты σ_ij пересчитываются по формуле, которая обобщает формулу (6) для преобразования компонент вектора 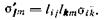(15)

Напомним, что так как здесь дважды повторяются индексы i и дважды повторяются индексы k, то по ним необходимо суммиро­вать. Следовательно, краткая запись по существу представляет собой двойную сумму.

Если набор из девяти величин (σ_ij) подчиняется преобразова­нию (15), то это может служить определением тензора (второго ранга). Если набор из трех величин (а_i) подчиняется преобразова­нию (6), то это служит определением вектора в трехмерном про­странстве. Если же численное значение а не меняется с преобразо­ванием координат, то это скаляр. Ранее упоминалась зависимость компонент от трех координат. В том случае, если рассматривается неустановившееся течение, они должны зависеть также от вре­мени.

Дата добавления: 2015-05-09