Упрощение булевых выражений

Таблицы истинности наряду с булевыми выражениями – удобный метод описания работы логических схем. Как правило, конструирование логических схем начинается с составления таблицы истинности, на базе которой составляется булево выражение. Зачастую оно получается сложным и приводит к созданию сложных схем. Рассмотрим пример. Необходимо составить логическую схему, используя булево выражение 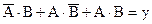. Для этого надо использовать три элемента И, два инвертора и один элемент ИЛИ с тремя входами. На рисунке 2.7 изображены схема, реализующая приведенное булево выражение, и таблица истинности.

В ней сразу можно узнать таблицу истинности для логического элемента ИЛИ с двумя входами. Упрощенное булево выражение с двумя входами есть 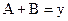. Такая схема с двумя входами и представлена на рисунке 2.7.

Этот пример показывает, что надо пытаться упростить заданное булево выражение, чтобы получить как можно более простую (а следовательно, и более дешевую) логическую схему. Для упрощения булевых выражений есть метод, который называется картами Карно. Кроме карт Карно, есть и другие методы упрощения булевых выражений: диаграммы Вейга, табличный метод.

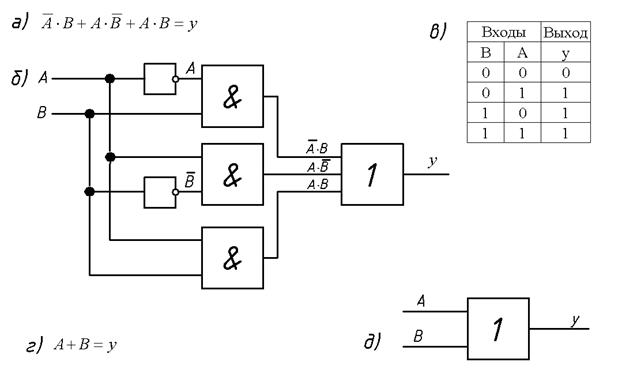
а – исходное булево выражение; б – логическая схема для булева выражения; в – таблица истинности; г – упрощенное булево выражение; д – логическая схема для упрощенного булева выражения.

Рисунок 2.7 – Упрощение булевых выражений

Рассмотрим таблицу истинности и карту Карно, представленную на рисунке 2.8. Четыре квадрата (1, 2, 3, 4) соответствуют четырем возможным комбинациям A и В в таблице истинности с двумя переменными. При таком изображении квадрат 1 на карте Карно соответствует произведению 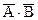, квадрат 2 ‑ произведению A ∙ 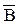и т.д.

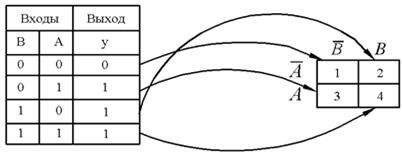
Рисунок 2.8 – Обозначение квадратов по карте Карно

Рассмотрим ранее представленную на рисунке 2.7 задачу с булевым выражением 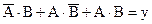. Заполним на нее карту Карно (рисунок 2.9).

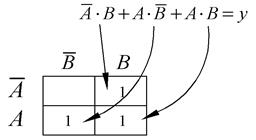
Рисунок 2.9 – Нанесение единиц на карту Карно

Произведем упрощение. В соответствии с правилами соседние единицы объединяются в один контур группами по две, четыре или восемь единиц. Построение контуров продолжается до тех пор, пока все единицы не окажутся внутри контуров. Каждый контур представляет собой новый член упрощенного булева выражения. На рисунке 2.10 получилось два контура, что означает: упрощенное выражение будет состоять только из двух членов, связанных функцией ИЛИ. Рассмотрим сначала нижний контур.

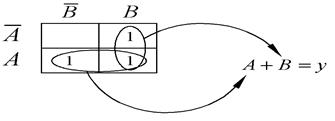
Рисунок 2.10 – Упрощение булевых выражений на основе карты Карно

Здесь Австречается в комбинации с и 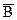. В соответствии с правилами булевой алгебры и 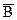дополняют друг друга и их можно опустить. Тогда в нижнем контуре остается только один член 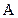. Аналогично этому вертикально расположенный контур содержит 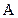и 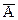, которые можно также опустить, оставив только В. Оставшиеся в результате 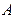и затем объединяются функцией ИЛИ, что приводит к упрощенному булеву выражению 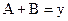.Упрощение булевых функций проводится в следующей последовательности.

1 Начинать надо с булева выражения в дизъюнктивной нормальной форме.

2 Нанести единицы на карту Карно.

3 Объединить соседние единицы контурами, охватывающими два или восемь квадратов.

4 Провести упрощения, исключая члены, дополняющие друг друга внутри контура.

5 Объединить оставшиеся члены (по одному в каждом контуре) функцией ИЛИ.

6 Записать полученное упрощенное булево выражение в дизъюнктивно-нормальной форме.

Дата добавления: 2015-05-09