
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференцирование сложной функции
|
|
|
|
ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ
Если функция y = f(x) обратима на интервале (а; b) и имеет отличную от нуля производную в некоторой точке х Î (а; b), то производная обратной функции равна обратной величине производной данной функции.
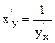
| или | 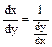
| ; | 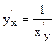
| или | 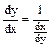
|
где индексы х и у показывают, по какой переменной производится дифференцирование, т.е. какая из переменных принята за независимую.
| КРАТКО: | Производные от взаимообратных функций обратны по величине. |
| Если y есть функция от u: y = f(u), где u в свою очередь есть функция от аргумента х: u = j(x), то у называется сложной функцией от х: y = f [j(x)]. | |||||
| y = f [j(x)] | - формула сложной функции | ||||
| х | - | независимая переменная (аргумент) | |||
| u = j(x) | - | промежуточная («внутренняя») функция | |||
| y = f(x) | - | сложная функция («внешняя») | |||
| КРАТКО: | y = f [j(x)] | Þ | y = f(u), где u = j(x) | ||
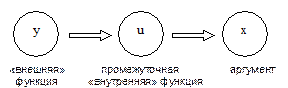
НАПРИМЕР: Разложить сложную функцию на составляющие функции
| 1) | 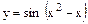
| 
| у = sin u, где u = x2 - x | |||||||
| 2) | 
| 
| у = u3, где u = 4х - 1 | |||||||
| 3) | 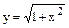
| 
| 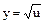 , где u = 1 + x2 , где u = 1 + x2
| |||||||
| 4) | 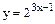
| 
| y = 2u, где u = 3х - 1 | |||||||
| 5) | 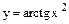
| 
| y = arctg u, где u = х2 | |||||||
| 6) | 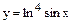
| 
| 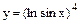  у = u4, где u = ln sin x у = u4, где u = ln sin x
| |||||||
 u = ln t, где t = sin x
u, t – промежуточные, «внутренние» функции u = ln t, где t = sin x
u, t – промежуточные, «внутренние» функции
| ||||||||||
| Производная сложной функции Для того, чтобы продифференцировать сложную функцию y = f [j(x)], нужно взять производную «внешней» функции f, рассматривая ее аргумент j(х) = u просто как переменную, по которой совершается дифференцирование, и умножить на производную от «внутренней» функции j(х) по независимой переменной. | ||||||||||
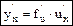
| или | 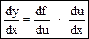
| ||||||||
| ПРАВИЛО | Производная сложной функции равна производной заданной функции по промежуточному аргументу, умноженной на производную этого аргумента по независимой переменной. | |||||||||
Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих.
| Алгоритм дифференцирования сложной функции | ||
| Разложить сложную функцию на составляющие и ввести новую переменную | 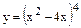 у = u4, где u = x2 – 4x
у = u4, где u = x2 – 4x
| |
| Записать сложную функцию через новую переменную | у = u4 | |
| Найти производную от новой (промежуточной) перемен-ной, а т.к. функция сложная, то умножить еще на производную промежу-точной «внутренней» переменной | 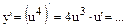
| |
| Ввести обратную замену (заменить промежуточную переменную) и найти производную промежу-точной («внутренней») переменной | 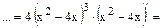
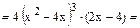
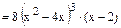
| |
| Найти значение производной в точке х = х0, если она указана | 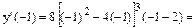
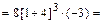
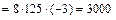 Ответ: y’(-1) = 3000
Ответ: y’(-1) = 3000
|
|
|
|
|
|
Дата добавления: 2015-05-10; Просмотров: 334; Нарушение авторских прав?; Мы поможем в написании вашей работы!