Квадратурні формули Ньютона-Котеса

Розглянемо інтерполяційні квадратурні формули, в яких вузли x_k Î[а;b] рівновіддалені. Такі формули називаються формулами Ньютона-Котеса. Їх вперше розглянув Ньютон, а коефіцієнти для них при n ≤9 знайшов Котес. Дослідження таких, формул показали, що коли n ≥10, то серед коефіцієнтів A_k є від’ємні і 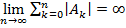. Отже, при великих n похибка квадратурної суми буде великою навіть при малих похибках в значеннях функції f (x_k). Тому на практиці квадратурні формули Ньютона-Котеса для великих n не використовуються. Розглянемо частинні випадки формул Ньютона-Котеса.

Вважатимемо, що для формул Ньютона-Котеса, які містять не менш як два доданки (n ≥1), вузли x_k розміщено такі що x ₀= a, x_n = b, x_{k +1}= x_k + h (k =0,1,…, n -1).

Крок h в даному випадку дорівнює . У випадку n =0 за єдиний вузол x ₀ можна взяти будь-яку точку на відрізку [ а; b ].

Квадратурні формули прямокутників. Нехай n =0, тоді формула (2), (3) набирає вигляду:

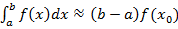(4)

Ця формула називається формулою прямокутників. Поклавши x ₀= a, або x ₀= b, або , дістанемо три формули прямокутників (лівих, правих і середніх відповідно).

Загальні формули прямокутників. Якщо відрізок інтегрування [ а; b ] великий, то похибка формули (4) може бути досить значною. Щоб цьому запобігти, розбивають відрізок на частини і застосовують формули до кожної з них. Розділимо, наприклад, відрізок інтегрування [ а; b ] на m рівних частин: [ x ₀; x ₁], [ x ₁; x ₂],..., [ x_{m -1}; x_m ], завдовжки 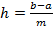, де x ₀= a, x_m = b. За властивістю інтеграла маємо: .

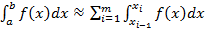Наприклад, позначивши 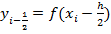(i =1,2,…, m) обчисливши кожний з інтегралів 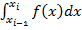(i =1,2,…, m) за формулою середніх прямокутників, матимемо:

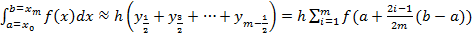(5)

Формулу (5) називають узагальненою формулою середніх прямокутників. Аналогічно дістанемо узагальнені формули лівих і правих прямокутників.

Квадратурна формула трапеції. Розглянемо випадок квадратурної формули Ньютона-Котеса, яка має два вузли x ₀= a і x_n = b (n =1). Коефіцієнти A_k (k =0,1) знаходимо з формули (3)

;

;

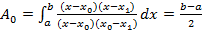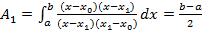Тоді формула (2) набирає вигляду:

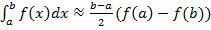(6)

Ми дістали квадратурну формулу, замінивши функцію f (x) інтерполяційним многочленом першого степеня (лінійна інтерполяція), який в точках x = a і x = b набуває відповідно значень f (a) і f (b). Формула (6) називається квадратурною формулою трапецій.

Узагальнена квадратурна формула трапецій. Якщо відрізок [ а; b ] великий, то й похибка формули (6) може бути великою. Щоб зменшити її, поділимо відрізок інтегрування [ а; b ] на m рівних частин: [ x ₀; x ₁], [ x ₁; x ₂],..., [ x_{m -1}; x_m ], завдовжки 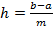причому x ₀= a, x_m = b. Тоді 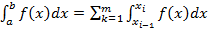. До кожного з m інтегралів застосуємо формулу (6). Дістанемо:

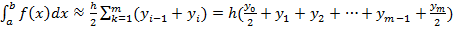, (7),

де y_i = f (x_i). Формула (7) називається узагальненою формулою трапецій.

Квадратурна формула Сімпсона. Розглянемо ще один приклад квадратурної формули Ньютона-Котеса, яка широко використовується на практиці і називається квадратурною формулою парабол, або формулою Сімпсона. Цю формулу дістанемо з (2), (3), якщо n =2. Вузлами тут є точки x ₀= a, 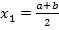, x ₂= b. Знайдемо коефіцієнти формули.

;

;

.

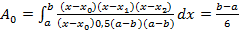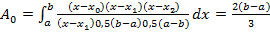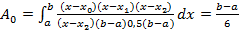Таким чином, формула Сімпсона має вигляд:

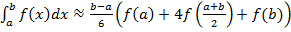(8)

У випадку додатної функції f(x) формула (8), як бачимо, зводиться до того, що інтеграл наближено замінюється площею фігури; яка обмежена віссю Ох, прямими х = а і х = b і параболою, що проходить через точки (a; f (a)), 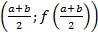, (b; f (b)).

Узагальнена формула Сімпсона. Якщо відрізок [ а; b ] великий, то його ділять на парну кількість 2 m рівних частин: [ x ₀; x ₁], [ x ₁; x ₂],..., [ x _{2 m -1}; x _{2 m} ] завдовжки 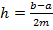(тут x ₀= a, x _{2 m} = b) і до кожних двох сусідніх відрізків завдовжки 2 h застосовують формулу Сімпсона (8). Тоді

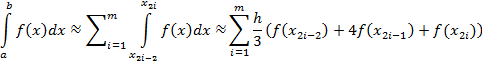
або

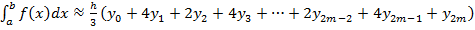(9)

де y_i = f (x_i), 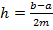. Формула (9) називається узагальненою формулою Сімпсона, або формулою парабол.

Дата добавления: 2015-05-10