Оцінка похибки інтерполяційного многочлена Лагранжа

Побудований для функції y=f(x) інтерполяційний многочлен Лагранжа n -го степеня у вузлах інтерполювання x ₀, x ₁,..., x _n збігається з функцією y = f (x). В інших точках відрізка [ a, b ] він відрізняється від функції y = f (x).

Величина R _n(x)= f (x)– L _n(x), яка характеризує близькість полінома L _n(x) до функції f(x) у деякій точці відрізка [ a, b ], називається залишковим членом інтерполяційного поліному Лагранжа. Знайдемо вираз для залишкового члена для функцій f (x), які на відрізку [ a, b ], що містить вузли інтерполювання, мають неперервні похідні до (n +1)-го порядку включно.

Оскільки залишковий член у вузлах інтерполювання дорівнює нулю, то можна записати:

f (x)– L _n(x)=(x – x ₀)(x – x ₁)(x – x ₂)...(x – x _n) k (x)=П_n+1(x) k (x), (7)

де k (x) – невідома функція. Для знаходження k (x) розглянемо допоміжну функцію u (t)= f (t)– L _n(t)–П_n+1(t) k (x), де x відіграє роль параметра. Тут за x візьмемо точку, в якій потрібно обчислити залишковий член інтерполяційного многочлена.

За рівністю (7) функція u (t) дорівнює нулю, якщо t = x ₀, x ₁,..., x _n і якщо t = x, тобто має на відрізку [ a, b ] принаймні n +2 нулі. Отже, на кінцях кожного з відрізків [ x ₀; x ₁], [ x ₁; x ₂],...,[ x _i; x ], [ x; x _i+1],...,[ x _{n – 1}; x _n] функція u (t) набуває значень рівних нулю. За теоремою Ролля всередині кожного з цих відрізків знайдеться принаймні одна точка, яка буде нулем похідної u `(t). Отже похідна u `(t) має на відрізку [ a, b ] принаймні n +1 нуль. Міркуючи аналогічно, встановлюємо, що u ``(t) на [ a, b ] має принаймні n нулів. Нарешті, u ⁽ⁿ⁺¹⁾(t) має на [ a,b ] принаймні один нуль x: u ⁽ⁿ⁺¹⁾(x)=0.

Оскільки , , 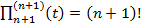то для u ⁽ⁿ⁺¹⁾(t) маємо: u ⁽ⁿ⁺¹⁾(t)= f ⁽ⁿ⁺¹⁾(t)–(n +1)! k (x). Отже, при t =x дістаємо: 0= f ⁽ⁿ⁺¹⁾(x)–(n+1)! k(x). Звідси .

Підставивши в рівність (7) значення k (x), дістанемо вираз для залишкового члена інтерполяційного многочлена L _n(x):

, (8)

де xÎ[a,b]. З формули (8) можна записати таку оцінку для R_n(x):

, де

У процесі обчислень виникають також неусувна похибка, оскільки значення часто даються наближено, і похибка округлення проміжних результатів. Останню можна звести до мінімуму, якщо обчислення виконувати з більшою кількістю цифр, ніж це вимагається для табличних значень функції. В остаточному результаті запасні цифри округлюють. Якщо оперувати усіма розрядами ЕОМ, то похибкою округлень проміжних результатів можна ігнорувати.

«Метод найменших квадратів»

Дата добавления: 2015-05-10