Метод хорд

Метод поділу проміжку пополам

Нехай на проміжку [ а; b ] функція f (х) неперервна і набуває на кінцях проміжку значень різних знаків, тобто f (а)× f (b)<0. Це означає, що на [ а; b ] рівняння має принаймні один корінь. Цей корінь можна визначити з наперед заданою точністю методом поділу проміжку пополам.

Суть методу полягає в тому, що проміжок, на якому міститься корінь, поступово звужують, зменшуючи його щоразу вдвоє, поки не досягнуть потрібної точності визначення кореня.

Позначимо лівий кінець проміжку, на якому міститься корінь, буквою u, правий – буквою v і знайдемо середину цього проміжку: 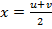. Оскільки (за умовою) f (u) f (v)<0, то f (х) f (а)>0 або f (х) f (а)<0, або f (х) = 0. Якщо f (х) = 0, то корінь х*=х. Зрозуміло, що у випадку f (х) f (а)>0 корінь міститься на проміжку [ x, v ]. У випадку f (х) f (а)<0 корінь міститься на проміжку [ u, х ]. Якщо довжина проміжку, на якому міститься корінь, не перевищує заданої величини e, то це означає, що х * знайдено з точністю до e. Якщо заданої точності ще не досягнуто, то, позначивши х через u у випадку f (х) f (а)>0 або через v у випадку f (х) f (а)<0, знову знаходимо середину проміжку [ u; v ] і повторюємо обчислення.

Методом хорд (його ще називають методом лінійного інтерполювання) нове значення х знаходять як абсцису точки перетину хорди, що проходить через точки (u; f (u)), (v; f (v)), з віссю О х. При цьому f (u) f (v)<0.

Рівняння згаданої хорди, виходячи з рівняння прямої, що проходить через дві точки, матиме вигляд:

або .

Звідси знаходимо абсцису точки перетину хорди з віссю Ох (рівняння якої у =0), тобто покладаємо у =0 і визначаємо з даного рівняння х:

.

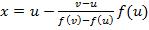Якщо f (х) f (u)>0, то корінь міститься на проміжку [ x;v ], тому щойно знайдений х беремо за нове значення лівого кінця проміжку, на якому міститься корінь. Якщо f (х) f (u)<0, то корінь міститься на проміжку [ u;х ], тому х беремо за нове значення правого кінця проміжку, на якому міститься корінь.

Якщо f (х)=0 або нове значення х практично не відрізняється від попереднього значення х, то можна вважати, що х – наближення кореня х*.

Метод дотичних (Ньютона)

Нехай функція f (x) двічі неперервно диференційована на проміжку [ а;b ], причому похідні f '(x) і f'' (x) не дорівнюють нулеві і зберігають знак на цьому проміжку, а f (а) f (b)<0. При цьому змінна х наближається до кореня лише з одного боку (це стосується і методу січних).

За методом дотичних (методом Ньютона) наближене значення кореня х знаходять як абсцису точки перетину дотичної до кривої у = f (х) в одній з точок (u; f (u)) чи (v; f (v)) з віссю О х. Оцінку близькості х до кореня х *, як і раніше, можна проводити аналогічно до методу січних.

Першу дотичну треба проводити в тій точці (u; f (u)) чи (v; f (v)), для якої виконується умова: f (u) f'' (u)>0 чи f (v) f'' (v)>0. Нехай дотична проводиться в точці (u; f (u)). Тоді рівняння дотичної в цій точці матиме вигляд: y–f (u)= f' (u)(х – u). Звідси знаходимо абсцису точки перетину дотичної з віссю О х:

.

Якщо значення u вважати за початкове (нульове, позначимо його через х ₀) наближення до кореня х *, то значення х, знайдене за останньою формулою, вважатимемо новим наближенням (першим, позначимо його х ₁). Значення х ₁ можна уточнити, а саме: наступне наближення до кореня х * знову визначити як точку перетину дотичної до кривої у = f (x), проведеної в точці (х₁; f (х ₁)), з віссю абсцис. Отже, за методом Ньютона кожне наступне наближення до кореня х * знаходять за формулою

, k=0,1,2,…

причому х ₀= u, якщо f (u) f'' (u)>0, і х ₀= v, якщо f (v) f'' (v)>0.

Перевагою метода Ньютона є велика швидкість збіжності наближеного значення кореня до істинного. Недоліки - пристосовуваність лише для диференційовних функцій, необхідність задання додаткової функції - похідної від заданої, однобічність наближення коренів.

Розв’язання рiвнянь В процесі вивчення багатьох питань економіки, природознавства, техніки тощо доводиться розв’язувати системи лінійних алгебраїчних рівнянь. Зокрема, до таких систем зводиться чисельне розв’язування лінійних диференціальних та інтегральних рівнянь. Важливе практичне значення таких систем зумовило розробку чималого арсеналу різних методів розв’язування систем лінійних рівнянь. В своїй абсолютній більшості вони передбачають існування і єдність розв’язку і поділяються на точні та наближені методи. До точних належать метод Гаусса та його модифікації, правило Крамера, метод квадратних коренів тощо. До наближених – метод ітерації, метод Зейделя. Точні методи можна назвати точними лише умовно, бо початкові дані можуть бути наближеними числами і, крім цього, заокруглення в процесі проміжних обчислень приводяться до втрати точності кінцевого результату.

Метод Гаусса приваблює простотою алгоритму і невеликим числом в порівнянні з правилом Крамера проміжних обчислень. Метод квадратного кореня годиться лише для симетричної головної матриці системи рівнянь і практично не використовується.

Дата добавления: 2015-05-10