Інтерполяційний поліном Лагранжа

Нехай у точках x ₀, x ₁,..., x _n (x _i¹ x _j, якщо i ¹ j) з відрізка [ a, b ] задано значення функції y = f (x): y _i= f (x _i). Треба побудувати такий поліном L_n(x) = a₀+a₁ x +... +a_n x ⁿ (степеня, не вищого за n), який у вузлах x ₀, x ₁,..., x _n набуває тих самих значень, що й функція y= f (x), тобто

L_n(x _i) = f (x _i) (i =0, 1,..., n). (3)

З умови (3) для знаходження коефіцієнтів a_i (i =0, 1,..., n) дістаємо систему рівнянь:

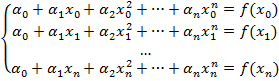(4)

Визначником цієї системи є визначник Ван дер Монда:

,

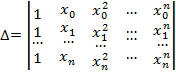який, як відомо, дорівнює 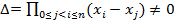. Це означає, що функції 1, x, x ²,..., x ⁿ утворюють систему Чебишева. Отже, система (4) має єдиний розв’язок при будь-яких значеннях f (x _i) (i =0, 1,..., n). Таким чином, коли серед вузлів немає таких, що збігаються, то алгебраїчний многочлен існує і єдиний.

Щоб дістати інтерполяційний многочлен у явному вигляді, не станемо розв’язувати систему (4), а побудуємо безпосередньо многочлен L _n(x), який задовольняє умову (3). Многочлен L _n(x) шукатимемо у вигляді лінійної комбінації деяких многочленів степеня n, причому коефіцієнтами цієї лінійної комбінації будуть задані значення функції y=f(x) у вузлах, тобто

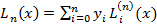(5)

де 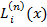(i =0, 1,..., n) – поки що невідомі многочлени степеня n.

З умови (3) випливає, що многочлени 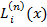мають задовольняти умову

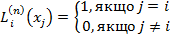, тобто

.

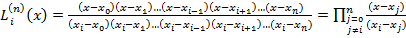Підставивши вирази 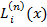у формулу (5), дістанемо вираз інтерполяційного многочлена L_n(x):

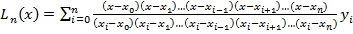(6)

Інтерполяційний многочлен, записаний у вигляді (6), називається інтерполяційним многочленом Лагранжа. Многочлени 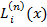називаються коефіцієнтами Лагранжа.

Запишемо формулу Лагранжа для випадку рівновіддалених вузлів. Нехай x ₁– x ₀= x ₂ – x ₁ =... = x _n– x _n–1= h. Для спрощення зробимо заміну x = x ₀+ th. Тоді x – x _k= h (t – k) і інтерполяційний поліном Лагранжа матиме вид:

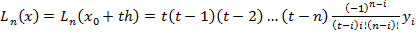, де t =(x – x ₀)/ h.

Дата добавления: 2015-05-10