Постановка задачі

Часто задачі зводяться до відшукання розв’язку певного диференціального рівняння (або системи таких рівнянь), який задовольняє певні початкові умови (задача Коші). Проінтегрувати таке рівняння в скінченому вигляді вдається досить рідко. На практиці здебільшого застосовують наближене інтегрування диференціальних рівнянь.

Задача Коші для диференціального рівняння 1-го порядку

(1)

полягає у відшуканні функції y = y (x), яка задовольняє цьому рівнянню і початковій умові

y (x ₀)= y ₀, (2)

де x ₀, y ₀ – задані числа.

Задача Коші для системи диференціальних рівнянь

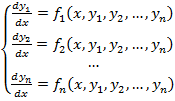(3)

полягає у відшуканні функції y ₁, y ₂,..., y_n, які задовольняють даній системі і початковим умовам

y ₁(x ₀)= y ₁₀, y ₂(x ₀)= y ₂₀,...., y_n (x ₀)= y_{n 0} (4)

Задача Коші для диференціального рівняння n -го порядку

y ⁽ⁿ⁾= f (x, y ¢, y ¢¢,..., y ^(n–1)) (5)

полягає у відшуканні функції y = y (x), що задовольняє рівняння (5) і початковим умовам

y (x ₀)= y ₀, y ¢(x ₀)= y ¹₀,..., y ^{(n –1)}(x ₀)= y^{n –1}₀.

Наближені методи в залежності від форми, в якій вони подають розв’язок, можна поділити на дві групи: аналітичні методи, які дають наближений розв’язок диференціального рівняння у вигляді аналітичного виразу; чисельні методи, які дають наближений розв’язок у вигляді таблиці. Надалі припускається, що для розглядуваних рівнянь і систем рівнянь виконуються умови існування і єдності розв’язку.

Якщо відомий наближений розв’язок задачі (1)–(2) в точці х_к, то проінтегрувавши рівняння (1) в межах від х_к до х_к +1, знайдемо його розв’язок в точці х_к +1 за формулою

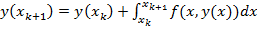(5)

Саме ця формула є вихідною для побудови багатьох чисельних методів розв’язування задачі (1)–(2).

Метод Ейлера. Якщо інтеграл в правій частині рівності (5) обчислити за формулою лівих прямокутників, то знайдемо

у (х_{к +1})= у (х_к)+ hf (х_к, у (х_к))+O(h ²).

Відкинувши в цій рівності доданок порядку O(h ²), дістанемо розрахункову формулу

у (х_{к +1})= у (х_к)+ hf (х_к, у (х_к)), (k =0,1,2,.., n –1), h = х_{к +1}– х_к, (6)

яку називають формулою Ейлера.

Якщо інтеграл в правій частині рівності (5) обчислити за формулою трапецій, то знайдемо

у (х_{к +1})= у (х_к)+ h(f (х_к, у (х_к))+f(х_к+1, у (х_к+1)))+O(h ³). (7)

Невідоме значення у (х_{к +1}), що входить до правої частини цієї рівності, можна обчислити за формулою (6). Підставивши його в праву частину рівності (7), дістанемо рівність

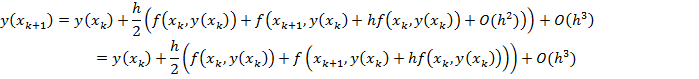
Звідси матимемо такі розрахункові формули

, ,

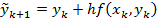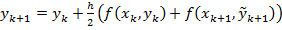які називають узагальненими формулами Ейлера-Коші.

Метод Ейлера легко переноситься на системи диференціальних рівнянь і на диференціальні рівняння вищих порядків. Розглянемо систему двох рівнянь першого порядку:

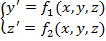
з початковими умовами y (x ₀)= y ₀, z (x ₀)= z ₀. Наближені значення y (x_i)= y_i i z (x_i)= z_i обчислюються за формулами

Для диференціального рівняння n -го порядку вводять заміну y ¢= y ₁, y’ ¢= y ₂,..., y ^{(n –1)}= y_{n –1} і приходять до задачі (3)–(4), де f ₁= y ₁, f ₂= y ₂,..., f_{n –1}= y_{n –1}, f_n (x, y ₁,..., y_{n –1}, y_n)= f (x, y ¢,..., y ^{(n –1)}, y).

Метод Рунге-Кутта. У роботі задача Коші розв’язувалась методами Ейлера. Однак вони дають порівняно великі похибки. Точнішими, хоча і громісткішими є методи Рунге-Кутта. Такі методи побудовано до 10-го порядку точності включно. В обчислювальній практиці найчастіше використовують методи Рунге-Кутта четвертого порядку точності. Алгоритм полягає у наступному.

Позначимо через h крок таблиці і побудуємо систему рівновіддалених точок x_i = x ₀+ ih (i =0,1,2...). За методом Ейлера наближене значення y (x_i)= y_i обчислюється послідовно за формулами:

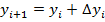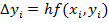, , i =0,1,2,

За методом Рунге-Кутта обчислення наближеного значення y_{i +1} в наступній точці x_{i +1}= x_i + h виконується за такою ж формулою як і при методі Ейлера: 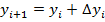. Однак 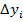обчислюється більш точно за формулою:

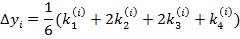
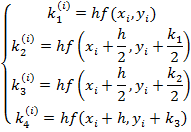
Іноді оцінити залишковий член квадратурної формули дуже важко або й неможливо, наприклад тоді, коли функцію задано таблично і аналітичний вираз її невідомий, або коли функцію задано складним аналітичним виразом і її похідні важко оцінити. Тоді використовують методи подвійного перерахунку, які передбачають двічі обчислювати означений інтеграл, але при різних h. Якщо результати практично рівні, то можна вважати, що обчислення проведено правильно і за остаточний результат взяти значення, обчислене при меншому кроці, а за похибку – різницю між одержаними значеннями.

Дата добавления: 2015-05-10