Дифференциальное уравнение теплопроводности

Для изучения закономерностей распространения теплоты в однородном и изотропном теле используют метод математической физики. Этот метод исходит из того, что ограничивается бесконечно малый промежуток времени и из всего пространства рассматривается лишь элементарный объем. Это позволяет пренебречь изменением теплофизических величин, характеризующих процесс.

Выбранные таким образом элементарный объем dv и элементарный промежуток времени dτ с математической точки зрения являются величинами бесконечно малыми, а с физической точки зрения – величинами еще достаточно большими, чтобы в их пределах можно было рассматривать среду как сплошную.

При решении задач, связанных с нахождением температурного поля, необходимо иметь дифференциальное уравнение теплопроводности. В основу вывода уравнения положен закон сохранения энергии: количество теплоты dQ, введенное в элементарный объем извне за время dτ вследствие теплопроводности, а также от внутренних источников теплоты, равно изменению внутренней энергии

, (1.1)

где dQ₁ – количество теплоты, Дж, введенное в элементарный объем путем теплопроводности за время dτ;

dQ₂ – количество теплоты, Дж, которое за время dτ выделилось в элементарном объеме за счет внутренних источников;

dQ – изменение внутренней энергии, Дж.

Для нахождения составляющих уравнения выделим в теле элементарный параллелепипед со сторонами dx, dy, dz.

По закону Фурье количество теплоты, проходящее за время d через грань dy-dz, вдоль оси x будет равно

.

Тепловой поток, проходящий через противоположную грань dy-dz, будет соответственно

.

Разница между количеством теплоты, подведенного к элементарному параллелепипеду, и количеством теплоты, отведенного от него за время dτ

.

Функция q_x+dx является непрерывной в рассматриваемом интервале dx и может быть разложена в ряд Тейлора

.

Если ограничиться двумя первыми членами ряда, то

.

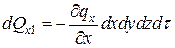Аналогичным образом можно найти количество теплоты, подводимое к элементарному объему в направлениях других координат у и z.

Тогда общее количество теплоты, подведенное к объему

.

Определим вторую составляющую уравнения dQ₂. Обозначим количество теплоты, выделяемое внутренними источниками в единице объема среды в единицу времени и называемое мощностью внутренних источников теплоты, через q_v, Вт/м³

.

Третья составляющая в уравнении для изохорного процесса, когда вся теплота уйдет на изменение внутренней энергии вещества dQ=dU, определится

.

Подставляя полученные выражения в уравнение (1.1) получаем

.

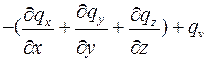Проекции вектора плотности теплового потока на координатные оси x,y,z

, , .

Дифференциальное уравнение теплопроводности в общем виде

+ .

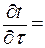
Обозначим: ,

.

С учетом введенных обозначений дифференциальное уравнение теплопроводности для нестационарного процесса с учетом внутренних источников теплоты

.

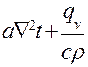Коэффициент пропорциональности а, м²/с, называется коэффициентом температуропроводности и является физическим параметром вещества. Если коэффициент теплопроводности характеризует способность тел проводить теплоту, то коэффициент температуропроводности является мерой теплоинерционных свойств тела. Выравнивание температуры тела будет проходить быстрее в том теле, где больше коэффициент а.

Если система не содержит внутренних источников теплоты (q_v=0), то дифференциальное уравнение теплопроводности имеет вид

.

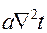Для стационарной теплопроводности и при отсутствии внутренних источников теплоты выражение принимает вид

.

Дата добавления: 2015-05-26