Условия однозначности для процессов теплопроводности

Дифференциальное уравнение теплопроводности описывает явление в самом общем виде, т.е описывает класс явлений теплопроводности. Чтобы рассмотреть конкретный процесс следует дать его полное математическое описание. Математическая постановка задачи включает в себя дифференциальное уравнение теплопроводности и условия однозначности. Частные особенности конкретного процесса теплопроводности называются условиями однозначности или краевыми условиями, которые включают в себя:

Геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс;

Физические условия, характеризующие физические свойства тела и окружающей среды;

Временные (начальные) условия, характеризующие распределение температур в теле в начальный момент времени;

Граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой.

Граничные условия могут быть заданы несколькими способами.

Граничные условия первого рода. Задается распределение температуры на поверхности тела для каждого момента времени

t_пов=f(х,у,z, ).

В частном случае, когда температура на поверхности является постоянной (для стационарной теплопроводности), то t_пов=const. Это условие обычно называют условием Дирихле.

К граничным условиям І рода можно отнести задачи разогрева системы при заданном изменении температуры на границе или при весьма интенсивном теплообмене.

Граничные условия второго рода. Задается значение плотности теплового потока для каждой точки поверхности и любого момента времени

q_пов = f(х,у,z, ).

В простейшем случае, для стационарной теплопроводности, когда плотность теплового потока по поверхности и во времени остается постоянной q_пов=const. Эти условия обычно называют условием Неймана.

Такой случай имеет место при нагревании изделий в высокотемпературных печах.

Граничные условия третьего рода. При этом задаются температура окружающей среды и закон теплообмена между поверхностью тела и окружающей средой. Процесс охлаждения или нагревания тел описывается законом Ньютона-Рихмана

,

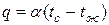где 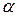- коэффициент теплоотдачи, характеризующий интенсивность теплообмена между поверхностью тела и окружающей средой. Коэффициент теплоотдачи зависит от большого числа факторов. Однако во многих случаях при решении задач теплопроводности его можно считать неизменным.

Плотность потока, подводимая за счет теплопроводности к поверхности тела, определяется по закону Фурье. Следовательно, на основании закона сохранения энергии

.

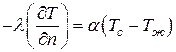Граничные условия четвертого рода (сопряжения). Задаются как условия равенства температуры и плотностей теплового потока на поверхности соприкосновения двух сред или тел

,

.

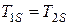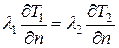Эти условия называют условиями идеального теплового контакта. Задачи с такими условиями ставятся при расчетах многослойных теплоизоляционных покрытий в металлургической, авиационной и космической технике.

Дата добавления: 2015-05-26