Передача теплоты через плоскую стенку

Тема 2 Теплопроводность при стационарном режиме

Вопросы к введению и теме 1.

1. Дайте определения основных видов теплообмена.

2. Что называется температурным полем? Дать определение стационарного и нестационарного температурного поля.

3. Что называют изотермической поверхностью и температурным градиентом?

4. Сформулируйте гипотезу Фурье, объясните знак «минус» в уравнении.

5. Что называют тепловым потоком?

6. Что такое коэффициент теплопроводности, его размерность. Поясните физический смысл.

7. От каких факторов зависит коэффициент теплопроводности? В каких пределах изменяется его значение для газов, жидких сред и твердых материалов?

8. Вывести дифференциальное уравнение теплопроводности. Проанализировать его.

9. Записать дифференциальное уравнение теплопроводности для стационарного и нестационарного процессов.

10. Что такое коэффициент температуропроводности, его размерность, что он характеризует?

11. Что значит сформулировать математическую постановку задачи?

12. Что включают в себя условия однозначности?

13. Как задаются граничные условия первого, второго и третьего родов?

14. Записать уравнение Ньютона-Рихмана. Дать определение коэффициента теплоотдачи, его размерность.

При стационарном тепловом режиме 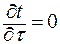. При этом дифференциальное уравнение теплопроводности

.

Если внутренние источники теплоты отсутствуют (q_v=0)

.

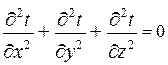Граничные условия первого рода. Теплопроводность однослойной плоской стенки. Рассмотрим однородную и изотропную стенку толщиной с постоянным коэффициентом теплопроводности 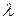. На наружных поверхностях стенки поддерживают постоянными температуры t_с1 и t_с2.

При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки, а в направлении осей y и z будет оставаться постоянной

.

В связи с этим дифференциальное уравнение теплопроводности запишется в виде

.

Граничные условия задаются следующим образом

х=0, t=t_с1,

х= , t=t_с2.

Это есть полная математическая формулировка данной задачи, в результате решения которой должны быть найдены распределение температуры в плоской стенке, а также получена формула для определения плотности теплового потока.

Закон распределения температур по толщине стенки найдется в результате двойного интегрирования.

Первое интегрирование дает .

После второго интегрирования: t=c₁x+c_2.

Постоянные с₁ и с₂ определим из граничных условий.

При х=0, t=t_с1 и с₂=t_c1; при х= , t=t_с2 и c₁= - .

Подставляя значения постоянных с₁ и с₂ в уравнение получаем закон распределения температуры в плоской стенке

_.

Для определения количества теплоты, проходящего через единицу поверхности стенки в единицу времени в направлении оси х, воспользуемся законом Фурье

.

Учитывая, что , после подстановки получаем

_.

Количество теплоты, проходящее через единицу поверхности стенки в единицу времени, прямо пропорционально коэффициенту теплопроводности 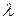, разности температур на наружных поверхностях стенки и обратно пропорционально толщине стенки . Тепловой поток определяется не абсолютным значением температур, а температурным напором t_c1- t_c2= .

Отношение , Вт/(м²К), называется тепловой проводимостью стенки, а обратная величина , (м²К)/Вт, - термическим сопротивлением стенки, которое представляет собой падение температуры в стенке на единицу плотности теплового потока.

Из уравнения температурного поля получаем

,

откуда следует, что температура в стенке убывает тем быстрее, чем больше плотность потока.

Теплопроводность многослойной плоской стенки. Рассмотрим теплопроводность многослойной стенки, состоящей из n однородных слоев. При стационарном режиме тепловой поток, проходящий через любую изотермическую поверхность неоднородной стенки, будет постоянен

.

При заданных температурах на внешних поверхностях такой стенки, размерах слоев и соответствующих коэффициентах теплопроводности, можно составить систему уравнений

.

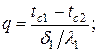
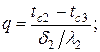
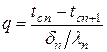Определив температурные напоры в каждом слое и сложив правые и левые части уравнений

.

Отсюда плотность теплового потока

.

Величина , равная сумме термических сопротивлений всех n слоев, называется полным термическим сопротивлением теплопроводности многослойной стенки.

При сравнении переноса теплоты через многослойную стенку и стенку из однородного материала удобно ввести эквивалентный коэффициент теплопроводности

.

Внутри каждого из слоев температура изменяется по линейному закону, а для многослойной стенки в целом температурная кривая представляет ломаную линию.

Граничные условия третьего рода (теплопередача). Передача теплоты из одной среды к другой через разделяющую их стенку однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной среде.

Теплопередача через плоскую однородную стенку. Пусть плоская однородная стенка имеет толщину . Коэффициент теплопроводности стенки , температуры окружающей среды t_ж1 и t_ж2, а также коэффициенты теплоотдачи ₁ и 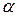₂ постоянны. Это позволяет рассматривать изменение температуры жидкостей и стенки только в направлении, перпендикулярном плоскости стенки.

При заданных условиях необходимо найти тепловой поток от горячей жидкости к холодной и температуры на поверхности стенки.

Согласно уравнению Ньютона-Рихмана плотность теплового потока от горячей жидкости к стенке

.

При стационарном тепловом режиме плотность теплового потока, обусловленная теплопроводностью через твердую стенку

.

Тепловой поток от второй поверхности стенки к холодной жидкости

.

Сложив почленно, и, выразив температурный напор

t_ж1 - t_ж2 = .

Отсюда плотность теплового потока

q = .

Обозначим

.

Тогда уравнение теплопередачи через плоскую однослойную стенку

.

Величина k называется коэффициентом теплопередачи, Вт/(м²К). Характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку и численно равен количеству теплоты, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус.

Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи

,

где - термическое сопротивление теплоотдачи от горячей жидкости к стенке; 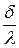- термическое сопротивление теплопроводности стенки; - термическое сопротивление теплоотдачи от стенки к холодной жидкости.

Теплопередача через плоскую многослойную стенку. Поскольку общее термическое сопротивление состоит из частных термических сопротивлений, то для многослойной стенки нужно учитывать термическое сопротивление каждого слоя

или .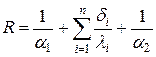

Отсюда

.

Плотность теплового потока через многослойную стенку, состоящую из n слоев

q = .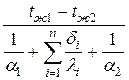

Уравнение теплопередачи для многослойной стенки подобно уравнению для однослойной стенки. Различие заключается в выражениях для коэффициентов теплопередачи.

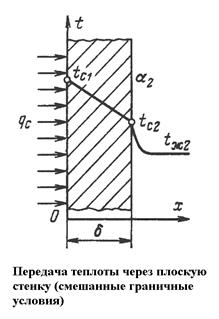Граничные условия второго и третьего рода. Заданы граничные условия второго рода на одной поверхности стенки в виде q_c = const; на другой поверхности заданы граничные условия третьего рода, то есть задан коэффициент теплоотдачи 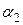и температура жидкости t_ж2. Внутренние источники теплоты в стенке отсутствуют q_v=0. Требуется найти распределение температур в стенке и температуры на ее поверхности.

Для стационарного теплового процесса

; .

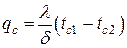Из этих уравнений следует, что при заданных значениях q_с могут быть определены температуры на поверхностях

t_c2 =t_ж2+ ; t_c1 = t_ж2+ .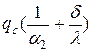

Для многослойной стенки: на внешних поверхностях

t_c(n+1) = t_ж2+ ; t_c1 = t_ж2+ ,

на поверхности между слоями

.

Дата добавления: 2015-05-26