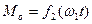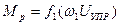Білет №27

АФХ системи

>

5. аперіодична ланка. Частота спряження визначається з співвідношення

w_cп = 1/Т. В даному випадку Т = 10, w_cп = 0,1. lg w_сп = -1. Асимптота піднята на висоту L = 20 Дб оскільки К=10, 20*lg 10=20. В точці спряження відбувається зміна нахилу асимптоти на значення – 20дб/дек.

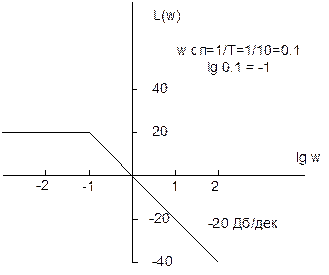
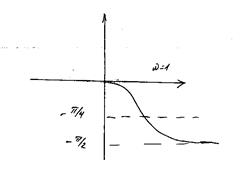
6. це ідеальна інтегруюча ланка, в якої значення Т = 1/100. w_cп = 1/Т = 100. В ідеальної інтегруючої ланки ФЧХ не залежить від Т і має вигляд прямої, яка проходить значення – π/2

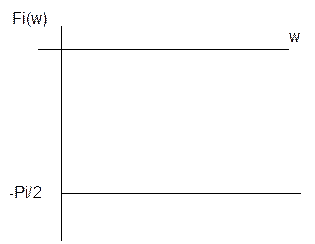
7) для критерію стійкості по Гурвіцу визначаємо значення визначників Гурвіца:

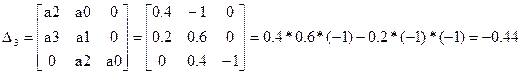
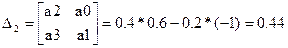
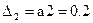
система нестійка

1. ЧУК.
2. Це ідеальна інтегруюча ланка з значенням параметра Т = 1:

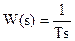
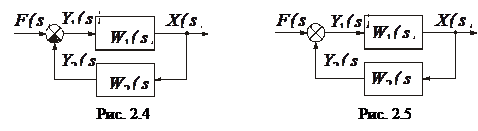3.

Для зустрічно-паралельного сполучення ланок з від’ємним зворотним з’язком (рис.2.4), маємо

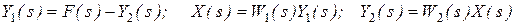. (2.45)

Виключивши проміжні змінні, отримаємо

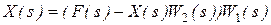, (2.46)

Звідки

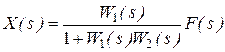. (2.47)

Порівнюючи рівняння (2.39), (2.47) отримаємо вираз для обчислення передатної функції зустрічно-паралельного сполучення ланок з від’ємним зворотним з’язком

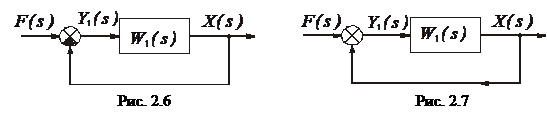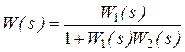. (2.48)

тут 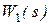- передатна функція основної ланки; 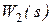- передатна функція ланки зворотнього зв’язку. У випадку додатного зворотнього зв’язку (рис. 2.5), вираз (2.48) набуде вигляду

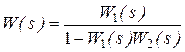. (2.49)

Зворотний зв’язок може бути одиничним, тобто, коли вихідний сигнал безпосередньо без проміжних перетворень подається на елемент порівняння (рис. 2.6, 2.7), тоді у виразах (2.48), (2.49) відповідно, слід прийняти

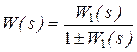. (2.50)

4.

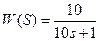
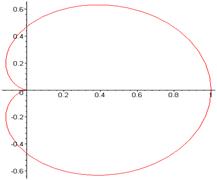
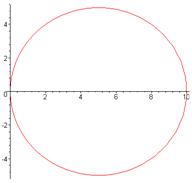
аперіодична ланка з колом радіусом k/2 = 5 з центром в точці U = 5, V = 0

K/2 =5

5.

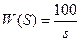
ідеальна інтегруюча ланка. ЇЇ ЛАЧХ матиме вигляд прямої під кутом -20Дб/дек, яка пересікає вісь Х в точці lg w, де w = 1/T. T =1/100, w =100. lg w = 2

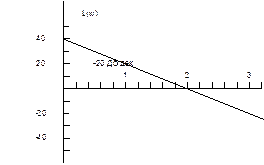
6.

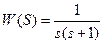
це дві ланки: ідеальна інтегруюча і аперіодична. Відповідно ФЧХ буде сумою ФЧХ окремих ланок:

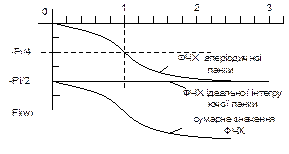
7. побудуємо матрицю Раусса

r	N стрічки	І	ІІ	ІІІ
-		0,5	0,5
-		0,5	0,5

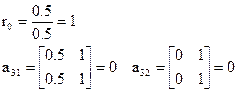система перебуває на границі стійкості

Білет № 28

1. Інтегруюча ланка описана рівнянням 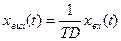називається ідеально інтегруючою ланкою, так як вона не може бути реалізована на практиці. Дійсно при t=0 має місце стрибок швидкості 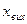від нуля до 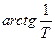. Отже, в початковий момент прискорення повинно бути нескінченно великим, що не може бути реалізовано на практиці.

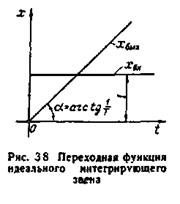
Реальні інтегруючі ланки можуть бути представлені у вигляді послідовно включених аперіодичної і ідеально інтегруючої ланок.

Передаточна функція реально інтегруючої ланки буде мати вигляд .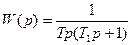

Прикладом реальних інтегруючих ланок є електродвигун, коли вхідна величина у них – напруга, а вихідна – кут повороту валу або пропорційна йому величина.

Передаточна функція реально інтегруючої ланки має вигляд .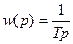

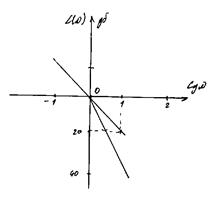
Амплітудно-фазова характеристика інтегруючої ланк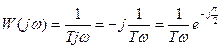и при 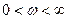являє собою пряму, співпадаючою з уявною відємною полувісю. Інтегруючу ланку інколи називають астатичною, поскільки в астатичних системах, як правило, є інтегруючі ланки.

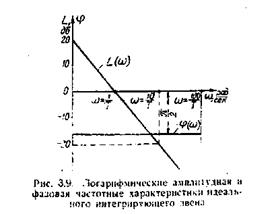
Визначимо логарифмічну амплітудно-частотну характеристику інтегруючої ланки. Так як 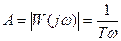, тому .

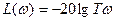Ця характеристика являє собою пряму, перетинаючи вісь абсциси в точці 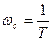. Нахил прямої рівний 20 дб на декаду.

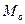дане рівняння є нелінійним бо і 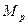є нелінійними.

В якісь точці зрівноваження 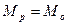і кутове прискорення стане рівне нулю,тобто швидкість стане сталою і двигун перейде в ітераційний режим.

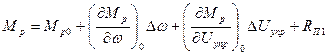де 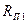- члени верхніх порядків малості

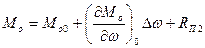
3. Інтегруючі, диференціюючі та пропорціональні елементи являються ланками автоматичної системи, тому будь-яка лінійна динамічна система може бути представлена тільки з елементів цього типу.

Дата добавления: 2015-05-26