Матрицы. Операции над матрицами

МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Литература: [1], Т.2, гл. 10,12; [6], гл. 1,2.

Матрицей размера или -матрицей называется прямоугольная таблица чисел

, (2.1)

состоящая из строк и 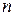столбцов.

Если 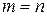, то матрица называется квадратной.

В сокращенной записи матрица (2.1) - , , .

Наряду с круглыми скобками применяют и другие обозначения матрицы: .

Матрица 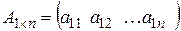называется матрицей (вектором)-строкой, а матрица, состоящая из одного столбца - матрицей(вектором)-столбцом:

-матрица-столбец.

Элементы матрицы , у которых номер столбца равен номеру строки , называются диагональными и образуют главную диагональ матрицы.

Матрица, у которой все недиагональные элементы равны нулю, называется диагональной.

Единичной матрицей называется квадратная диагональная матрица, у которой все диагональные элементы-единицы:

.

Нулевой матрицей называется матрица, все элементы которой равны нулю:

.

Две матрицы 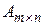и 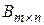одинаковой структуры равны, если они совпадают поэлементно, т.е .

Над матрицами можно производить ряд операций:

1.Произведением матрицы 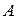на число называется матрица, элементы которой .

2. Суммой матриц и одного порядка называется матрица 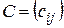того же порядка, каждый элемент которой равен сумме соответствующих элементов матриц 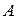и , т.е .

В частном случае .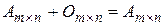

3. Разность двух матриц определяется через предыдущие операции: , где .

4. Произведение матрицы размера на матрицу размера , называется матрица 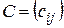размера , элемент которой

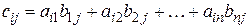(2.2)

Свойства, кроме коммутативного закона умножения, присущие операциям над действительными числами, справедливы и для операций над матрицами.

Пример 2.1. Найти произведение матриц и .

, .

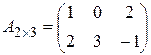Решени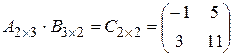е. .

, т.е. .

Пример 2.2. Найти произведение матриц и , если это возможно:

, .

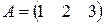Решение ;

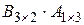-это произведение не существует.

Коммутативный закон выполняется, в частности, при умножении квадратных матриц 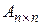на единичную матрицу :

5. Квадратные матрицы можно возводить в целую положительную степень : .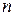

6. Следом квадратной матрицы 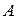называется сумма ее диагональных элементов: .

Пример 2.3. Возвести матрицу в степень и найти след матрицы .

Решение. , .

7. Транспонирование матрицы - переход от матрицы 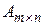к матрице , в которой строки и столбцы поменялись местами с сохранением порядка .

Свойства операций транспонирования:

1) . 3)

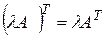2) . 4)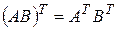

Пример 2.4. Даны матрицы и . Проверить свойство .

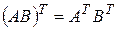Решение. , .

.

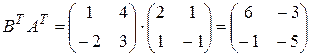№ 2.1. Найти сумму и разность матриц

, .

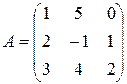№ 2.2. Найти матрицу , если

, .

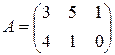№ 2.3. Найти произведение матриц , , если

, .

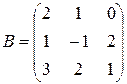Выполняется ли переместительный закон к произведению двух матриц?

№ 2.4. Найти произведение матрицы 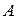на единичную матрицу слева и справа, если

.

Выполняется ли переместительный закон?

№ 2.5. Если можно, найти произведение матриц 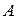и слева и справа:

а) , ;

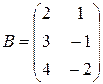б) , ;

в) , .

№ 2.6. Составить матричное равенство , если

, , .

№ 2.7. Дана матрица . Какую матрицу нужно прибавить к этой матрице, чтобы получить единичную матрицу ?

.

№ 2.8. Используя матрицу из предыдущего номера найти сумму .

№ 2.9. В матричном равенстве

найти и .

Дата добавления: 2015-05-26