
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определители. Решение системы линейных уравнений по формулам Крамера
|
|
|
|
Для характеристики квадратных матриц вводится числовой критерий-определитель.
Определителем второго порядка квадратной матрицы второго порядка 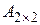 называется число, обозначаемое символом
называется число, обозначаемое символом 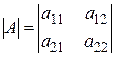 и определяемое равенством
и определяемое равенством
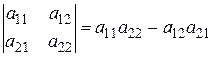 (2.3.)
(2.3.)
Определитель третьего порядка вычисляется по формуле
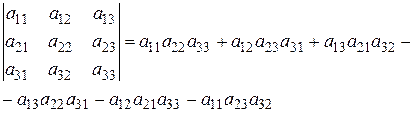 . (2.4.)
. (2.4.)
Определители матриц обозначаются символами 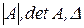 .
.
Для вычисления определителей третьего порядка по формуле (2.4.) применяют схему Сарруса:
 | |||
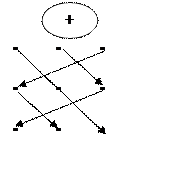 |
Соответствующие произведения элементов берутся со знаком <<+>> (левая схема), либо со знаком <<->> (правая схема).
Пример 2.4. Вычислить определитель  .
.
Решение. Применяя формулу (2.4.) по схеме Сарруса, получим
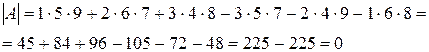 .
.
Определение определителя квадратной матрицы 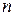 -го порядка сложное (см. стр.19 [6]).
-го порядка сложное (см. стр.19 [6]).
Минором  элемента
элемента  матрицы
матрицы 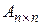 называется определитель матрицы
называется определитель матрицы 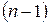 -го порядка, полученной из матрицы
-го порядка, полученной из матрицы 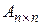 вычеркиванием
вычеркиванием  -ой строки и
-ой строки и 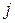 -ого столбца.
-ого столбца.
Например, минором элемента 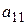 матрицы
матрицы 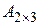 будет
будет


Алгебраическим дополнением 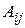 элемента
элемента  матрицы (определителя)
матрицы (определителя) 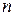 -го порядка называется его минор, взятый со знаком
-го порядка называется его минор, взятый со знаком 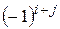 :
:
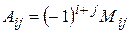 . (2.5.)
. (2.5.)
Например:
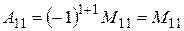 ,
, 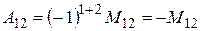 ,
,  .
.
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
 (2.6.)
(2.6.)
(разложение по элементам  -ой строки
-ой строки  ).
).
Разложение определителя по элементам 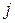 -го столбца имеет вид:
-го столбца имеет вид:
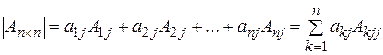 (2.7.)
(2.7.)
Для упрощения вычислений определителей применяются свойства:
1. Определитель не изменяется при транспонировании матриц, т.е. 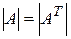 . строки и столбцы равноправны.
. строки и столбцы равноправны.
2. Если все элементы строки (столбца) умножить на одно и то же число, то определитель умножится на это число; общий множитель строки (столбца) можно вынести за знак определителя;
3. Определитель меняет знак, если поменять местами две строки (столбца);
4. Определитель равен нулю, если все элементы любой строки (столбца) равны нулю;
5. Определитель равен нулю, если элементы любых двух строк (столбцов) пропорциональны (равны);
6. Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить элементы другой строки (столбца), умноженное на число 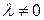 .
.
Пример 2.5. Вычислить определитель
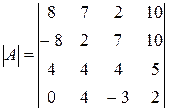 .
.
Решение. Из первого столбца вынесем общий множитель 4:

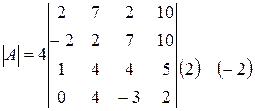 .
.
К первой строке прибавим третью строку, умноженную на (-2), ко второй строке прибавим удвоенную третью. Полученный определитель разложим по Теореме Лапласа по первому столбцу.
 .
.
Из третьей строки вынесем общий множитель 5 и из второго столбца 3. Имеем

 .
.
Третью строку, умноженную на (-2) прибавим ко второй строке и разлагаем по элементам третьего столбца:
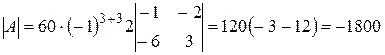 .
.
Решение системы 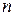 -линейных уравнений с
-линейных уравнений с 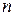 неизвестными
неизвестными
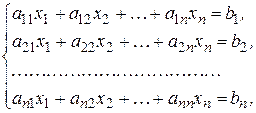 (2.8)
(2.8)
определитель которой  , находится по формулам Крамера
, находится по формулам Крамера
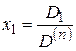 ,
, 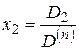 ,
, 
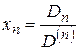 , (2.9)
, (2.9)
где  -определитель, полученный из. определителя системы заменой
-определитель, полученный из. определителя системы заменой 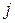 -го столбца столбцом свободных членов.
-го столбца столбцом свободных членов.
Пример 2.6. Решить систему по формулам Крамера:

Решение. Определитель матрицы

Вычисляем определители  ,
, 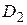 и
и  , заменяя в определителе
, заменяя в определителе 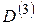 первый, второй и третий столбцы столбцом из свободных членов.
первый, второй и третий столбцы столбцом из свободных членов.
 .
.

 .
.
По формулам (2.9) получим 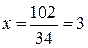 ,
, 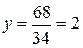 ,
,  .
.
№ 2.10. Вычислить определители 2-го и 3-го порядков по определению:
а)  ; б)
; б) 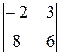 ; в)
; в)  ;
;
г) 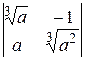 ; д)
; д)  ; е)
; е)  .
.
№ 2.11. Вычислить определители наиболее рациональным способом:
а) 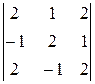 ; б)
; б) 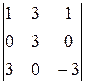 ; в)
; в) 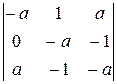 ;
;
г) 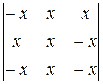 ; д)
; д)  ; е)
; е) 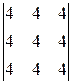 .
.
№ 2.12 Вычислить миноры и алгебраические дополнения элементов определителя из упражнений 2.11(б), 2.11(е).
№ 2.13. Составить определитель третьего порядка, равный нулю.
№ 2.14 Найти из уравнений 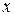 :
:
а) 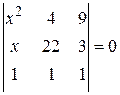 , б)
, б) 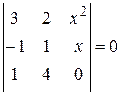
и проверить подстановкой корней в определитель.
№ 2.15. Вычислить определитель четвертого порядка в начале по формуле разложения по элементам первой строки, потом по свойствам:
а) 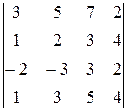 ; б)
; б) 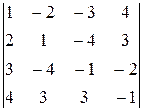 .
.
№ 2.16. Вычислить определители:
а)  ; б)
; б) 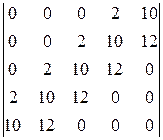 .
.
№ 2.17.-2.27 Решить системы уравнений по формулам Крамера:
№ 2.17.  № 2.18.
№ 2.18. 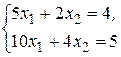
№ 2.19. 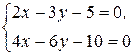 №2.20.
№2.20. 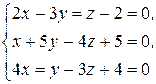
№ 2.21.  №2.22.
№2.22. 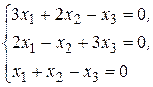
№ 2.23. 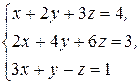 №2.24.
№2.24. 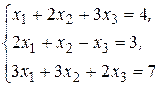
№2.25. 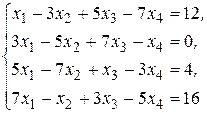 № 2.26.
№ 2.26. 
№2.27.  №.2.28
№.2.28 
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 730; Нарушение авторских прав?; Мы поможем в написании вашей работы!