Однородная система линейных уравнений

.

МЕТОД ГАУССА. ИССЛЕДОВАНИЕ РЕШЕНИЙ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С НЕИЗВЕСТНЫМИ

Метод Гаусса представляет систематизированную схему последовательного исключения переменных. Поясним смысл этого метода на системе с четырьмя неизвестными:

(2.13)

Допустим, что (если , то изменим порядок уравнений):

1 шаг: Делим первое уравнение на 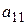, умножаем полученное уравнение на 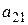и вычитаем из второго уравнения; затем умножаем на и вычитаем из третьего уравнения; наконец, умножаем на 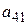и вычитаем из четвертого. в результате первого шага приходим к системе:

(2.14)

причем, получаются из по формуле:

,

,

2 шаг: Поступаем с системой (2.14) точно также, как с уравнениями системы (2.13) и т.д. в итоге исходная система преобразуется к треугольному виду

(2.15)

Из системы (2.15) все неизвестные определяются последовательно. Практически удобнее приводить к виду (2.15) не саму систему, а матрицу из коэффициентов при неизвестных и свободных членов (расширенную матрицу системы). Для контроля вводят 5-й столбец, каждым элементом которого является сумма пяти элементов данной строки. каждый элемент контрольного столбца преобразованной матрицы равен сумме элементов соответствующей строки.

Если система имеет единственное решение, то система приводится к треугольному виду.

В случае неопределенной системы треугольная система не получается, так как последнее уравнение содержит более одного неизвестного.

Если система несовместна, то после приведения к треугольному виду содержится хотя бы одно уравнение вида .

Пример. Решить систему уравнений:

Решение. Преобразуем матрицу в эквивалентную:

Мы поменяли местами первое и второе уравнение, тогда , что упрощает вычисления.

Вычитаем из остальных двух строк первую, умноженную соответственно на 3 и 4:

Изменив знаки во второй строке и умножив ее на 5, прибавляем к третьей строке:

(Мы разделили на 11 последнюю строку). Система приняла треугольный вид:

Последовательно находим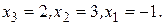

Дана система линейных уравнений с 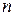неизвестными

(2.16)

Решением системы (2.16) называется совокупность 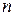чисел или 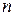-мерный вектор, которые будучи подставлены вместо неизвестных в уравнения системы, обращают их в тождества. Система (2.16) называется совместной, если она имеет хотя бы одно решение. Если же система не имеет ни одного решения, то она называется несовместной.

Совместная система называется определенной, если она имеет одно решение, неопределенной – если больше одного решения.

Матрицы

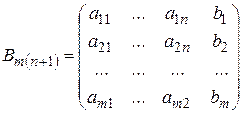, (.17)

называется соответственно матрицей системы и расширенной матрицей системы (2.16).

Теорема (Кронекера-Капелли) Для того, чтобы система (4.16) была совместной, необходимо и достаточно, чтобы .

В этом случае число называется рангом системы. Если , то система называется однородной. Однородная система уравнений всегда совместна, т.к. имеет тривиальное решение .

Если , то система является определенной. Если же ранг совместной системы меньше числа неизвестных, т.е. , то система неопределенная.

Пусть . Рассмотрим какой-нибудь базисный минор матрицы 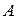. Выделим в этом миноре произвольную строку. Элементы этой строки являются коэффициентами при неизвестных в одном из уравнений системы. Эти неизвестных назовем базисными (основными) неизвестными рассматриваемой системы, остальные неизвестных системы назовем свободными (неосновными) неизвестными. Количество различных способов выбора переменных из общего числа 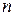конечно, оно равно числу сочетаний из 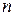элементов по в каждом, т.е.

.

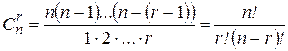Базисным решением системы 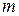линейных уравнений с 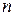неизвестными называется всякое ее решение, в котором свободные переменные имеют нулевые значения.

Выделим из системы (2.16) систему уравнений, среди которых содержатся элементы базисного минора. Базисные неизвестные оставим в левых частях уравнений, а члены, содержащие свободные неизвестные, перенесем вправо. Из полученной системы уравнений выразим базисные неизвестные через свободные неизвестные (например, по формулам Крамера).

Придавая свободным неизвестным произвольные значения, можно найти соответствующие значения базисных неизвестных. Система (2.16) имеет бесчисленное множество решений.

Пример. Исследовать систему уравнений

Решение. Здесь расширенная матрица системы

.

Вычтем из третьей строки первую:

,

разделим элементы третьей строки на 2 и вычтем из полученной третьей строки вторую; затем вычеркнем третью строку:

.

Нетрудно видеть, что . Следовательно, система совместна. Возьмем первое и второе уравнения заданной системы

За базисные неизвестные примем т.к. минор , т.е. является базисным. Свободными неизвестными служат и . Систему перепишем в виде

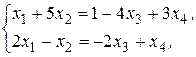
выразим 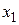и через и по формулам Крамера

Полагая и , получим решение системы в виде

, , , .

Придавая и 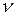различные значения, будем получать различные решения системы. В частности, первым базисным решением будет:

Аналогично можно найти другие базисные решения, их не более .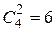

С помощью метода Гаусса можно решить и систему вида (2.16). С помощью элементарных преобразований расширенная матрица 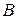может быть приведена к виду:

Если хотя бы одно из чисел 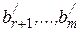отлично от нуля, то система не совместна.

Если же 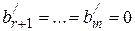, то система совместна и базисные неизвестные выражается через свободные .

Пример. Методом Гаусса найти решение системы

Решение. Произведя элементарные преобразования над расширенной матрицей 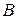, получим:

.

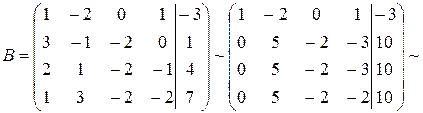
Первые две строки последней матрицы составляют расширенную матрицу систему:

эквивалентной исходной. Считая 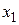, базисными неизвестными, а , - свободными, получим общее решение в виде:

, , , .

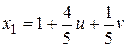№ 2.35. Решить по методу Гаусса систему 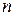линейных уравнений с 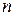неизвестными из №№ 2.20, 2.21, 2.23, 2.25, 2.26.

№ 2.36. Исследовать систему уравнений:

№ 2.37. Исследовать систему и найти хотя бы одно базисное решение

№ 2.38. Найти общее решение системы

№ 2.39-2.44. Исследовать совместимость и найти общее решение, базисные решения, допустимые базисные решения.

№ 2.39. №2.40.

№ 2.41. № 2.42.

№.2.43. № 2.44.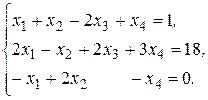

Система (2.16) называется однородной, если все свободные члены уравнения равны нулю:

(2.18)

Пусть и , тогда система (2.18) имеет единственное тривиальное решение (это условие означает, что ).

Однородная система имеет ненулевые решения, когда , при этом она имеет линейно независимых решений , где - решение записанное в виде строчной матрицы (вектора). Любое решение системы является линейной комбинацией решений . Набор решений называется фундаментальной системой решений системы.

Для нахождения фундаментальной системы решений свободные переменные поочередно заменяют элементами каждой строки единичной матрицы 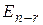порядка .

Пример. Решить однородную систему

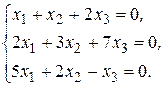
Решение. 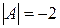, , 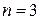. Система имеет только тривиальное(нулевое) решение .

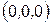Пример. Найти фундаментальную систему решений линейной системы и общее решение:

Решение. Систему решаем методом Гаусса.

. Базисных переменных 2, свободных переменных . За базисный минор принимаем , тогда , - базисные переменные, и - свободные. Система имеет вид:

откуда, полагая , , находим , .

Общее решение системы:

.

Из общего решения находим фундаментальную систему решений:

, .

Общее решение можно записать в виде:

.

Найти общее решение и фундаментальную систему следующих систем:

№ 2.45. № 2.26.

№ 2.47. 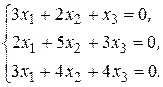№ 2.48.

№ 2.49.

№ 2.50.

Дата добавления: 2015-05-26