
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы линейного программирования
|
|
|
|
Литература: [1], т.2, гл. 14,13, [8 ], гл. 7,8.
Линейное программирование (ЛП), раздел математического программирования, является теоретической основой решения задач оптимального планирования.
Общая задача ЛП сводится к отысканию такого решения  системы
системы  линейных уравнений с
линейных уравнений с  переменными (система ограничений)
переменными (система ограничений)
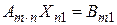 ,
,
 , (6.1)
, (6.1)
при котором целевая функция(линейная форма)
 (6.2)
(6.2)
принимает экстремальное значение. Здесь
 ,
,
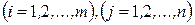
матрица условий задачи,

вектор ограничений.
Такое задание (постановка) задачи ЛП называется каноническим.
Чтобы найти это оптимальное решение среди бесчисленного множества допустимых решений систем ограничений (6.1), будем опираться на основные теоремы линейного программирования.
Теорема 1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.
Теорема 2. Если существует, и притом единственное, оптимальное решение задачи линейного программирования, то оно совпадает с одной из угловых точек множества допустимых решений.
Теорема 3. Каждому допустимому базисному решению задачи линейного программирования соответствует угловая точка области допустимых решений системы ограничений.
Теорема 4. (обратная) Каждой угловой точке множества допустимых решений системы ограничений соответствует допустимое базисное решение, число которых не более  .
.
Из теорем 2 и 4 вытекает:
Следствие. Если существует, и притом единственное оптимальное решение задачи ЛП, то оно совпадает с одним из допустимых базисных решений системы ограничений.
В простейших случаях оптимум линейной формы (6.2) (при  ) можно отыскать, используя геометрическое представление систем ограничений и линейной формы.
) можно отыскать, используя геометрическое представление систем ограничений и линейной формы.
|
|
|
Пример 6.1. Найти максимум функции
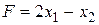 (6.3)
(6.3)
при ограничениях
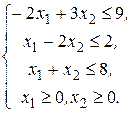 (6.4)
(6.4)
Убедиться в справедливости теорем 1-4.
Решение. На рис. 6.1. изображена область допустимых решений данной системы неравенств. Это выпуклый многоугольник  , имеющий пять угловых точек
, имеющий пять угловых точек  ,
,  ,
,  ,
,  ,
,  .
.

Множество допустимых решений выпукло (теорема 1).
Построим линии уровня целевой функции 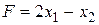 , которые определяются прямыми
, которые определяются прямыми  . При изменении
. При изменении 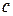 получаются параллельные прямые с нормалью
получаются параллельные прямые с нормалью  .
.
Пусть  , тогда прямая
, тогда прямая  проходит через начало координат. Перпендикулярно вектору
проходит через начало координат. Перпендикулярно вектору 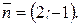
При переходе от одной линии уровня к другой значение функции  изменяется. Если исходную линию передвигать в направлении нормали
изменяется. Если исходную линию передвигать в направлении нормали  то значение
то значение  при этом возрастает.
при этом возрастает.
При этом легко видеть, что максимальное значение линейной формы на многоугольнике решений будет достигнуто в угловой точке  , в которой линия уровня при дальнейшем передвижении выйдет из этого многоугольника.
, в которой линия уровня при дальнейшем передвижении выйдет из этого многоугольника.
Следовательно, линейная форма достигает максимального значения в угловой точке  многоугольника решений:
многоугольника решений:
 .
.
Тем саамы подтверждается справедливость теоремы 2.
Систему ограничений(6.4.), введя добавочные неотрицательные переменные  сведем к системе трех уравнений с пятью неизвестными:
сведем к системе трех уравнений с пятью неизвестными:
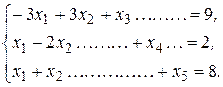 (6.5.)
(6.5.)
Система (6.5) может иметь не более 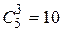 базисных решений. Найдем некоторые из них. Пусть
базисных решений. Найдем некоторые из них. Пусть  - основные переменные. Это можно сделать, поскольку коэффициенты при них образуют базисный минор, отличный от нуля. Приравняв свободные переменные
- основные переменные. Это можно сделать, поскольку коэффициенты при них образуют базисный минор, отличный от нуля. Приравняв свободные переменные 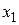 и
и  к нулю, получим базисное решение
к нулю, получим базисное решение  . Первые две компоненты в этом решении являются координатами
. Первые две компоненты в этом решении являются координатами  и
и 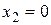 , что соответствует угловой точке
, что соответствует угловой точке  (теорема 3). Если за основные переменные принять
(теорема 3). Если за основные переменные принять  , то получим базисное решение
, то получим базисное решение 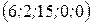 , которое соответствует угловой точке
, которое соответствует угловой точке  . Аналогично можно показать, что остальным точкам
. Аналогично можно показать, что остальным точкам  и
и  соответствуют допустимые базисные решения. остальные пять базисных решений являются недопустимыми. Возможны случаи, когда система ограничений несовместна или оптимальное решение неединственное.
соответствуют допустимые базисные решения. остальные пять базисных решений являются недопустимыми. Возможны случаи, когда система ограничений несовместна или оптимальное решение неединственное.
|
|
|
Геометрический метод пригоден и в случае, когда число переменных на два превышает число уравнений, то есть число свободных переменным равно двум.
Симплексный метод является универсальным методом, которым можно решить любую задачу линейного программирования. Есть различные модификации этого метода. Рассмотрим метод из [1,т.2,гл.IV].
Пример 6.2. Для изготовления шкафов и буфетов мебельная фабрика применяет древесину четырех видов, запасы которых ограничены и составляют соответственно 120, 160, 120 и 80 единиц. Матрица условий дана в таблице. Требуется составить такой план выпуска продукции, который бы обеспечил максимальную прибыль.
| Вид сырья | Запасы древесины | Технологические коэффициенты для производства единицы продукции | |
| шкафы | буфеты | ||
| I | |||
| II | |||
| III | |||
| IV | |||
| Прибыль |
Решение. Составим математическую модель задачи.
Пусть 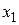 и
и  - соответственно количество шкафов и буфетов, запланированных к производству. Так как количество древесины по виду ограничено, то должны выполняться условия:
- соответственно количество шкафов и буфетов, запланированных к производству. Так как количество древесины по виду ограничено, то должны выполняться условия:
 (6.6.)
(6.6.)
Система (6.6.) является системой ограничения задачи. Целевая функция, выражающая прибыль предприятия, имеет вид:
 (6.7.)
(6.7.)
Приведем задачу к канонической форме. Найти максимум функции  (6.7.) при ограничениях
(6.7.) при ограничениях
 (6.8.)
(6.8.)
Так как в системе (6.8.)  и
и  , то число базисных переменных должно равняться четырем, а число свободных – двум.
, то число базисных переменных должно равняться четырем, а число свободных – двум.
Прежде всего, нужно найти любое базисное решение. В данном случае это легко сделать. Для этого достаточно взять в качестве базисных добавочные переменные, так как коэффициенты при них образуют единичную матрицу, определитель который равен единице. Считая 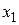 и
и  свободными переменными, равными нулю, получим базисное решение:
свободными переменными, равными нулю, получим базисное решение:
 ,
,
которое допустимо. Поэтому отпадает надобность в применении первого этапа симплексного метода.
Переходим ко второму этапу.
Первый шаг. Основные переменные  ; свободные переменные
; свободные переменные 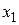 и
и  . В системе (6.8.) основные переменные выразим через свободные. Через свободные переменные выразим и линейную форму. Тогда получим
. В системе (6.8.) основные переменные выразим через свободные. Через свободные переменные выразим и линейную форму. Тогда получим

 .
.
При 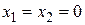 имеем
имеем 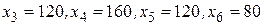 ,что дает исходное базисное решение
,что дает исходное базисное решение  . Значение линейной формы
. Значение линейной формы 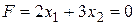 .
.
|
|
|
Когда мы полагаем 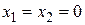 (фабрика ничего не выпускает), мы ставим цель – найти первое, безразлично какое, базисное решение. Эта цель достигнута. Теперь от этого решения нужно перейти к другому, при котором значение линейной формы увеличится. Из рассмотрения линейной формы видно, что ее значение возрастает при увеличении значений переменных
(фабрика ничего не выпускает), мы ставим цель – найти первое, безразлично какое, базисное решение. Эта цель достигнута. Теперь от этого решения нужно перейти к другому, при котором значение линейной формы увеличится. Из рассмотрения линейной формы видно, что ее значение возрастает при увеличении значений переменных 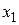 и
и  . Эти переменные надо перевести в основные, что означает переход к новому базисному решению. При симплексном методе на каждом шаге предполагается перевод в число основных только одной из свободных переменных. Переведем в число основных
. Эти переменные надо перевести в основные, что означает переход к новому базисному решению. При симплексном методе на каждом шаге предполагается перевод в число основных только одной из свободных переменных. Переведем в число основных  , так как она входит в линейную форму с большим коэффициентом.
, так как она входит в линейную форму с большим коэффициентом.
Как только одна из свободных переменных переходит в число основных, одна из основных должна быть переведена на ее место в число свободных. Какую же из четырех основных переменных нужно вывести?
Приведем следующие рассуждения. Значение  необходимо сделать как можно большим, так как это соответствует цели – максимизации
необходимо сделать как можно большим, так как это соответствует цели – максимизации  . Однако оказывается, что увеличение
. Однако оказывается, что увеличение  может продолжаться только до известных границ в силу условий (6.9.), пока не нарушится требование неотрицательности. Из каждого уравнения найдем отношение свободных членов к коэффициентам при
может продолжаться только до известных границ в силу условий (6.9.), пока не нарушится требование неотрицательности. Из каждого уравнения найдем отношение свободных членов к коэффициентам при  , получим
, получим 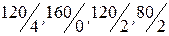 .
.
Для ответа на вопрос, какую переменную нужно перевести в число свободных, нужно принять
 .
.
Тогда 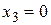 и
и  переходит в число неосновных переменных, а
переходит в число неосновных переменных, а 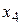 и
и  ,
,  останутся положительными.
останутся положительными.
Второй шаг. Основные переменные  ,
, 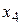 ,
,  ,
,  . Свободные переменные
. Свободные переменные 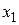
 . Дальше повторяется алгоритм первого шага. Выразим основные переменные и линейную форму через свободные переменные. Первое уравнение заключаем в рамку, считаем ведущим уравнением. Получим:
. Дальше повторяется алгоритм первого шага. Выразим основные переменные и линейную форму через свободные переменные. Первое уравнение заключаем в рамку, считаем ведущим уравнением. Получим:


При  имеем
имеем  . Это уже лучше, чем на первом шаге, но не искомый максимум. Дальнейшее увеличение
. Это уже лучше, чем на первом шаге, но не искомый максимум. Дальнейшее увеличение  возможно за счет введения переменной
возможно за счет введения переменной 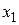 в число основных, так как она входит в линейную форму с положительным коэффициентом. для ответа на вопрос, какую переменную вывести из основных, примем
в число основных, так как она входит в линейную форму с положительным коэффициентом. для ответа на вопрос, какую переменную вывести из основных, примем

Тогда  и
и  переходит в число свободных, а
переходит в число свободных, а  и
и 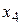 ,
,  останутся положительными. ведущее уравнение четвертое.
останутся положительными. ведущее уравнение четвертое.
|
|
|
Третий шаг. Основные переменные 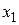 ,
,  ,
, 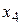 ,
,  . Свободные переменные
. Свободные переменные  . Получим:
. Получим:

 .
.
Из выражения линейной формы видно, что ее максимальное значение еще не получено, так как возможно увеличение  за счет введения в основные переменной
за счет введения в основные переменной  . Полагаем
. Полагаем

Здесь мы имеем два новых положения.
Во-первых, хотя переменная  и входит в выражение для
и входит в выражение для 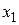 , но имеем положительный коэффициент и при любом возрастании
, но имеем положительный коэффициент и при любом возрастании  переменная
переменная 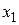 не может стать отрицательной, поэтому условно пишем
не может стать отрицательной, поэтому условно пишем  .
.
Во-вторых, мы получим два одинаковых минимальных значения. Если  , то
, то 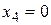 и
и  , то есть напрашивается вывод, что вместо одной переменной нужно перевести в число свободных сразу
, то есть напрашивается вывод, что вместо одной переменной нужно перевести в число свободных сразу 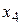 и
и  . Но число основных переменных не должно быть меньше четырех. как же быть в этом случае? Одну из переменных (
. Но число основных переменных не должно быть меньше четырех. как же быть в этом случае? Одну из переменных (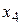 или
или  ) оставляем в числе основных, считая ее значение равным нулю, то есть полученное базисное решение будет вырожденным.
) оставляем в числе основных, считая ее значение равным нулю, то есть полученное базисное решение будет вырожденным.
Четвертый шаг. Основные переменные  свободные переменные
свободные переменные  . Имеем
. Имеем

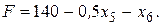
Так как в линейную форму переменные  входят с отрицательными коэффициентами, то никакое увеличение
входят с отрицательными коэффициентами, то никакое увеличение  за счет этих переменных невозможно.
за счет этих переменных невозможно.
Выполняется критерий оптимальности.
Отсутствие на каком-то шаге симплексного метода в выражении линейной формы  , максимум (минимум) которой ищется, свободных переменных с положительными (отрицательными) коэффициентами является критерий оптимальности.
, максимум (минимум) которой ищется, свободных переменных с положительными (отрицательными) коэффициентами является критерий оптимальности.
Следовательно, на четвертом шаге задача решена. Оптимальным является решение  , при котором
, при котором  . Фабрика должна изготовить 40 шкафов и 20 буфетов, прибыль будет 140 денежных единиц.
. Фабрика должна изготовить 40 шкафов и 20 буфетов, прибыль будет 140 денежных единиц.
Составить экономико–математические модели задач и привести к каноническому виду.
№ 6.1. Для выпуска изделий двух типов 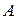 и
и  на фабрике используется сырье четырех видов. Расход сырья каждого вида на изготовление единицы продукции, запасы сырья, прибыль с одного изделия заданы таблицей 6.1.
на фабрике используется сырье четырех видов. Расход сырья каждого вида на изготовление единицы продукции, запасы сырья, прибыль с одного изделия заданы таблицей 6.1.
Таблица 6.1.
| Изделие | Сырье (расход сырья на изготовление единицы продукции) | Прибыль | |||
| I | II | III | IV | ||
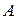

| 3 ден.ед. 2 ден. ед. | ||||
| Запасы сырья | 21 ед. | 8 ед. | 12 ед. | 5 ед. |
Составить план производства, обеспечивающий наибольшую прибыль.
№ 6.2. Совхоз закупает удобрения двух видов. В единице массы удобрения I содержится 3 усл. единицы химического вещества 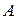 , 2 усл. единицы вещества
, 2 усл. единицы вещества  и 1-вещества
и 1-вещества  ; в единице массы удобрения II вида- 1 усл. единицы вещества
; в единице массы удобрения II вида- 1 усл. единицы вещества 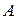 , 1 - вещества
, 1 - вещества  , 6-вещества
, 6-вещества  . На 1га почвы необходимо внести не менее 9 усл. единиц вещества
. На 1га почвы необходимо внести не менее 9 усл. единиц вещества 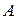 , 8- вещества
, 8- вещества  , 6-вещества
, 6-вещества  . Составить наиболее экономичный план закупки удобрений (в расчете на 1га), если цена удобрений (на 1 единицу массы) для I вида составляет 3 ден. единицы, а для II вида – 2 ден. единицы.
. Составить наиболее экономичный план закупки удобрений (в расчете на 1га), если цена удобрений (на 1 единицу массы) для I вида составляет 3 ден. единицы, а для II вида – 2 ден. единицы.
№ 6.3. На четырех станках (I, II, III, IV) обрабатываются два вида деталей (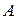 и
и  ), причем каждая деталь проходит обработку на всех станках. Время обработки деталей на каждом станке, время работы станков в течение одного цикла производства и прибыль, полученная от выпуска деталей каждого вида даны в таблице 6.2.
), причем каждая деталь проходит обработку на всех станках. Время обработки деталей на каждом станке, время работы станков в течение одного цикла производства и прибыль, полученная от выпуска деталей каждого вида даны в таблице 6.2.
Таблица 6.2.
| Станки | Время обработки детали, ч | Время работы станка за цикл производства | |
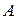
| 
| ||
| I II III IV | |||
| Прибыль |
Составить план производства, обеспечивающий наибольшую прибыль при условии, что количество деталей вида  не должно быть меньше деталей вида
не должно быть меньше деталей вида 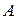 .
.
№ 6.4. Для производства стали определенной марки, в которую в качестве легирующих веществ должны входить химические элементы  , можно закупить шихту двух видов (I и II). В таблице 6.3. указано, сколько требуется каждого из этих элементов для производства 100 тонн стали (по технологии можно немного больше, но меньше нельзя), содержание этих элементов в каждой тонне шихты, а также стоимость 1 тонны шихты.
, можно закупить шихту двух видов (I и II). В таблице 6.3. указано, сколько требуется каждого из этих элементов для производства 100 тонн стали (по технологии можно немного больше, но меньше нельзя), содержание этих элементов в каждой тонне шихты, а также стоимость 1 тонны шихты.
Таблица 6.3.
| Вид шихты | Стоимость 1 т шихты | Легирующие вещества | ||

| 
| 
| ||
| I II | 3 ден. ед. 2 ден. ед. | |||
| Необходимое количество легирующих веществ |
Определите наименьшие затраты для производства стали данной марки.
№ 6.5. (Задача составления рациона). При откорме каждое животное ежедневно должно получить не менее 9 ед. питательного вещества 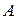 , не менее 12 ед. вещества
, не менее 12 ед. вещества  , и не менее 12 ед. вещества
, и не менее 12 ед. вещества  . Для составления рациона используют два вида корма. Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма указаны в таблице 6.4.
. Для составления рациона используют два вида корма. Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма указаны в таблице 6.4.
Таблица 6.4.
| Питательные вещества | Количество единиц в 1 кг корма | |
| Корм I | Корм II | |


| ||
| Стоимость 1 кг |
Составить дневной рацион так, чтобы затраты были минимальными.
Геометрически решить задачу линейного программирования
№ 6.6. Решить геометрически № 6.1, № 6.3, № 6.5.
Найти максимум функции  при заданных ограничениях:
при заданных ограничениях:
№ 6.7. 

№ 6.9. 

№ 6.11. 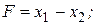

№ 6.8. 

№ 6.7. 
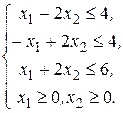
№ 6.12. 

Найти минимум функции  при заданных ограничениях:
при заданных ограничениях:
№ 6.13. 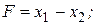

№ 6.15. 

№ 6.14. 
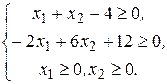
№ 6.16. 

№ 6.17. Проверить основные теоремы линейного программирования на примере задач № 6.8, № 6.10, № 6.12.
№ 6.18. Решить симплексным методом задачи № 6.1-6.5.
Решить, используя симплексный метод
№ 6.19.  № 6.20.
№ 6.20. 



№ 6.21.  №6.22
№6.22 


№ 6.23.  №6.24
№6.24 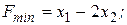


№6.25.  №6.26.
№6.26. 


№6.27.  №6.28.
№6.28. 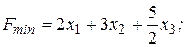


|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 2533; Нарушение авторских прав?; Мы поможем в написании вашей работы!