Поверхности второго порядка

I. Цилиндры второго порядка

Цилиндрической поверхностью второго порядка называется поверхность, которая образуется движением прямой (образующей) параллельно координатной оси, сохраняя постоянное направление и пересекая каждый раз неподвижную кривую второго порядка (направляющую), лежащей на координатной плоскости.

Беря за направляющие различные кривые второго порядка, и принимая направление оси 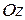за направление образующих этих цилиндров, мы получим цилиндрические поверхности (Рис. 5.1-5.3):

1. Эллиптический цилиндр:

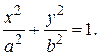
При 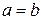получим круговой цилиндр с уравнением .

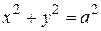2. Гиперболический цилиндр:

3. Параболический цилиндр:

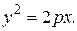
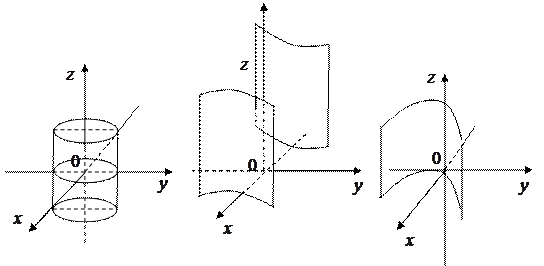
Рис. 5.1 Рис. 5.2 Рис. 5.3

II. Поверхности вращения.

Поверхностью вращения называют поверхность, образованную вращением некоторой плоской кривой вокруг координатной оси, лежащей в ее плоскости.

Уравнения поверхностей, образованных вращением кривых второго порядка вокруг их осей симметрии, если ось вращения , кривые расположены на плоскости , находят по формуле

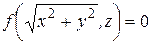
1. Эллипсоид вращения. Вращая эллипс 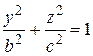, лежащий на плоскости 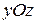вокруг оси 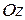, получим поверхность

,

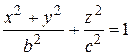которая называется эллипсоидом вращения (Рис 5.4)

2. Гиперболоид вращения. Беря в плоскости 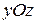две сопряженные гиперболы, осью которых служит ось , ,

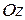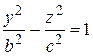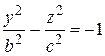
и вращая их вокруг оси 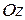, получим две поверхности:

,

.

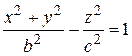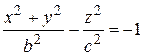Первая из них называется однополостным гиперболоидом вращения (Рис 5.5), вторая –двуполостным гиперболоидом вращения (Рис 5.6.).

Вращая вокруг оси 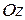пару общих асимптот этих гипербол 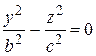, получим конус вращения (Рис 5.7.)

.

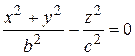3. Параболоид вращения. Уравнение параболы, лежащей в плоскости 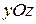, осью которой служит 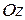, имев вид 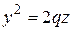. Параболоид вращения имеет уравнение(Рис.5.7.)

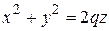
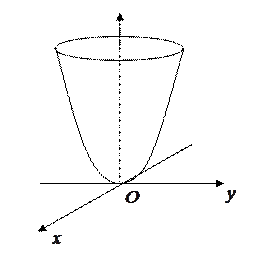
Рис. 5.7.

Сечения поверхностей вращения плоскостями, перпендикулярными оси вращения, являются окружностями. Такие поверхности являются частными случаями поверхностей второго порядка общего вида, в сечении которых соответствующими плоскостями получаются эллипсы. Например, эллипсоид имеет уравнение

.

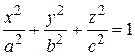Кроме пяти поверхностей вращения второго порядка и трех цилиндров второго порядка существует, еще одна- девятая поверхность второго рода, которую называют гиперболическим параболоидом. Уравнение этой поверхности:

.

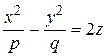Общее уравнение поверхностей второго порядка имеет следующий вид:

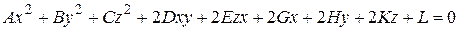(5.8)

Для упрощения таких уравнений пользуются методами квадратичных форм:

В зависимости от собственных чисел матрицы квадратичной формы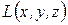

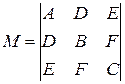
общее уравнение (5.8.) приводится к каноническим формам уравнений поверхностей второго порядка.

Это следующие поверхности с каноническими уравнениями.

1. Эллипсоид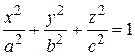

2. Однополостный гиперболоид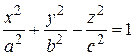

3. Двуполостной гиперболоид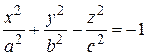

4. Конус,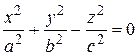

5. Эллиптический параболоид .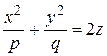

№ 5.62. построить поверхности:

1) ;

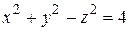2) .

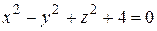№ 5.63. Назвать и построить каждую из поверхностей:

1)

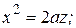
3)

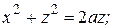
5)

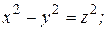
2)

4)

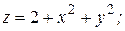
6)

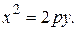
№ 5.64. Найти центр и радиус сферы

.

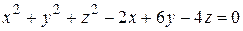№ 5.65. Найти центр и полуоси эллипсоида

.

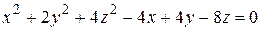№ 5.66. Написать уравнение геометрического места точек, одинаково удаленных от прямой 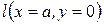и плоскости 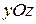. Построить поверхность.

№ 5.67. Написать уравнение геометрического места точек, одинаково удаленных от точки 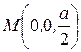и от плоскости 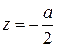. Построить поверхность.

№ 5.68. Написать уравнение поверхностей, образованных вращением кривых второго порядка

а) вокруг оси ,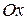

б) вокруг оси .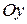

Построить тела, ограниченные поверхностями

№ 5.69.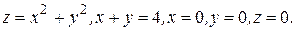

№ 5.70.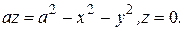

№ 5.71.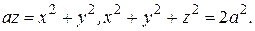

№ 5.72.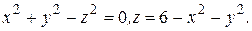

Дата добавления: 2015-05-26