Алгебраические уравнения и его корни

Задачу «найти все корни данного многочлена 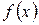» принято также формулировать следующим образом: «решить уравнение ».

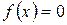Например, говоря о квадратном уравнении

,

мы тем самым ставим задачу найти корни квадратного трехчлена 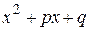. Корни многочлена называются также корнями уравнения .

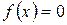Алгебраическим уравнением 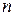-ой степени называется уравнение

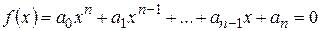. (1.18)

При решении уравнений (1.18.) полезна рассмотренная теорема Безу.

Теорема 1. Если 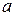-корень многочлена 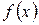, то этот многочлен делится на .

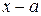Теорема 2. Пусть 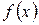и - два произвольных многочлена. Число 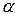в том и только в том случае является корнем уравнения 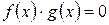, если оно является корнем хотя бы одного из уравнений , .

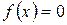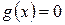Из этой теоремы вытекает важное следствие. Если 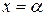корень уравнения 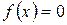, то 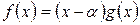и нахождение остальных корней уравнения сводится к решению уравнения 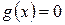, степень которого .

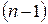Из свойств многочленов и формул Виета следует теорема 3.

Теорема 3. Если все коэффициенты многочлена 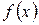является целыми и 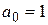, то всякий целый корень уравнения является делителем 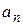свободного члена.

Эта теорема облегчает отыскание целых корней алгебраических уравнений (1.18.) с целыми коэффициентами. Надо взять свободный член и выписать все его делители. После этого надо проверить, какие из них являются корнями уравнения. Если же окажется, что ни один делитель не обращает многочлен в нуль, то уравнение целых корней не имеет.

Пример 1.12. Решить уравнение .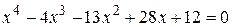

Решение. Свободный член 12 имеет делители:

.

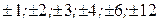Подставим эти числа в многочлен, находим:

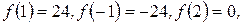т.е. 2 есть корень многочлена. Итак, один корень найден. По теореме 1, многочлен 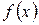делится на . Произведя деление («в столбик»), находим

.

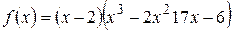Для нахождения остальных корней нужно решить уравнение

.

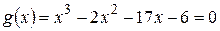Опять выписываем делители свободного члена 6:

.

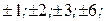Числа 1 и -1 не могут быть корнями, т.к. они не являются корнями исходного уравнения. Испытав дальнейшие делители, получим:

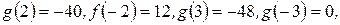т.е. (-3) есть корень многочлена .

По теореме 1 многочлен делится на 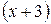. Произведя деление, находим

.

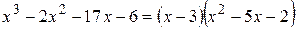Значит, для нахождения оставшихся корней нужно решить квадратное уравнение 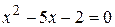. Это дает еще два корня: 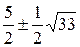. Таким образом, исходное уравнение имеет четыре корня:

.

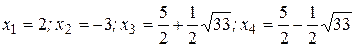Из основной теоремы алгебры следует

Теорема 4. Каждое алгебраическое уравнение 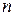-ой степени имеет ровно 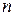корней.

№1.14. Уравнение 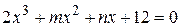имеет корни 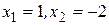. Найдите третий корень этого уравнения.

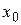№1.15. Вычислите сумму , если - корень уравнения .

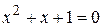Указание. Вычислите .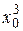

№1.16. При каком условии 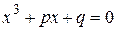имеет два равных корня?

Указание. Применяйте формулы Виета.

№1.17. Докажите, что всякое алгебраическое уравнение нечетной степени с действительными коэффициентами имеет хотя бы один действительный корень.

№1.18. Все коэффициенты уравнения

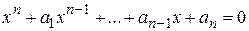
-целые числа. Докажите, что любой рациональный корень этого уравнения является целым числом.

№1.19. Решите уравнения:

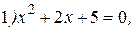
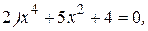
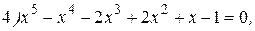
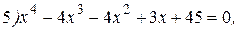
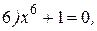
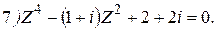
Дата добавления: 2015-05-26