Конечномерное пространство

Определение: Система векторов линейного пространства V над числовым полем Р называется линейно зависимой, если можно подобрать такие числа из поля Р, среди которых по меньшей мере одно отлично от нуля, что. Если же равенство возможно только в том случае, когда все числа равны нулю, то система векторов называется линейно независимой.

Линейная зависимость

Перейдём к понятию линейной зависимости, играющему важную роль в теории линейных пространств.

Пример. Пусть V – вещественное пространство трехмерных строк. Возьмем следующую систему векторов этого пространства:

, , .

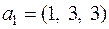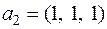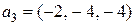Нетрудно заметить, что .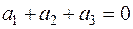

Таким образом, рассматриваемая система векторов линейно зависима. Однако, любая пара ее векторов будет уже линейно независима. В самом деле, если бы, например, пара векторов 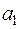и 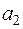была линейно зависимой, то имело бы место равенство 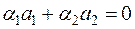, в котором хотя бы одно из вещественных чисел 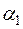и 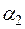отлично от нуля. Пусть для определенности 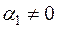. Тогда 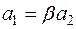, где 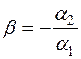. Отсюда строка 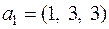была бы пропорциональна строке 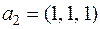, чего на самом деле нет.

Система векторов, в частности, может состоять из одного вектора a. Легко видеть, что такая система линейно зависима тогда и только тогда, когда 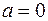, т.е. когда a – нулевой вектор. Вещественно, равенство 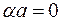возможно только пр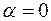и или 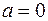. Если 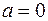, то 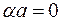при любом числе .

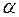Исходя из определения линейной зависимости, можно сделать следующие выводы.

1. Если система т векторов 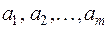линейно независима, то любая часть этой системы будет линейно независимой.

В самом деле, возьмем для определенности 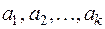(k<m) и покажем, что эта часть системы векторов 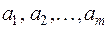будет также линейно независимой. Предположим «противное»: пусть она линейно зависима. Тогда будет иметь место равенство 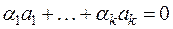, в котором по меньшей мере одно из чисел 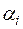(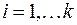), не равно нулю. Это равенство можно переписать следующим образом:

,

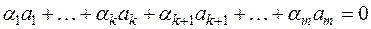полагая 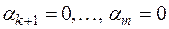. Но последнее равенство свидетельствует о том, что система векторов 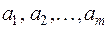линейно зависима, что невозможно.

2. Пусть для системы векторов 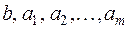имеет место равенство

,

где 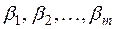– некоторые числа из Р (часть из них и даже все могут быть равными нулю). Мы будем в таком случае говорить, что вектор b является линейной комбинацией векторов.

Имеет место критерий линейной зависимости: система векторов 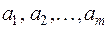в случае тогда и только тогда линейно зависима, когда по меньшей мере один вектор этой системы есть линейная комбинация остальных векторов.

Действительно, если система векторов 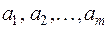линейно зависима, то имеет место равенство 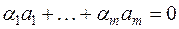, в котором хотя бы один из коэффициентов 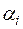отличен от нуля. Пусть, например, 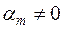. Тогда 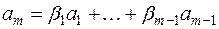, где 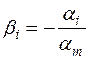, (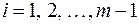) т.е. вектор 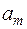является линейной комбинацией остальных векторов системы.

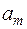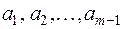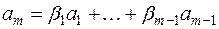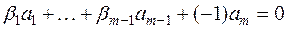Обратно, если, например, вектор является линейной комбинацией векторов : , то , т.е. система векторов 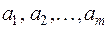линейно зависима, т.к. коэффициент при 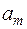отличен от нуля.

Пример. Рассмотрим следующую систему векторов вещественного пространства четырёхмерных строк:

, , ,

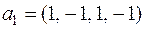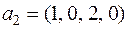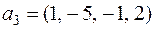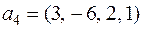
Эта система линейно зависима, т.к.

.

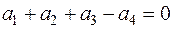Мы видим, что любой вектор системы можно линейно выразить через ее остальные векторы. Например, .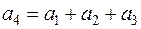

Дальнейшие свойства линейной зависимости тесно связаны с понятием ранга.

Под рангом системы векторов подразумевается максимальное число линейно независимых векторов этой системы.

В частности, ранг системы 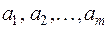, состоящей только из нулевых векторов, считается равным нулю.

Пример 1. Найдем ранг системы векторов 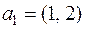, , 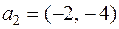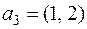вещественного пространства двумерных строк.

Прежде всего видим, что вся система линейно зависима:

.

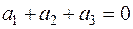Затем нетрудно заметить, что каждая пара векторов системы также линейно зависима:

, , .

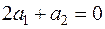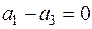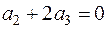Однако каждый вектор системы уже линейно независим, так как отличен от нулевого вектора. Следовательно, ранг данной системы векторов равен единице.

Пример 2. Легко убедиться, что ранг системы векторов 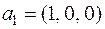, , 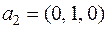, 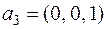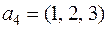вещественного пространства трехмерных строк равен трем.

В самом деле, вся система векторов линейно зависима:

.

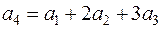Однако первые три вектора 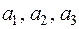линейно независимы, так как, подставляя в равенство 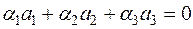выражения векторов 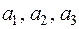получаем: 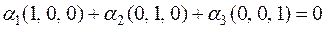, откуда , , .

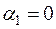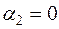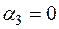Обратимся теперь к прямоугольной матрице

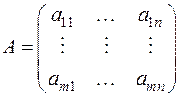
размера 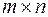элементов из числового поля Р. Будем рассматривать ее строки как векторы пространства n -мерных строк над полем Р, а столбцы – как векторы пространства m -мерных столбцов над полем Р. В дальнейшем нам понадобятся свойства линейной зависимости, связанные с рангом матрицы А.

Теорема 1. Если ранг матрицы А равен r, то существует r линейно независимых строк (столбцов} матрицы, через которые линейно выражаются остальные строки (столбцы) матрицы А. Эти линейно независимые строки (столбцы) проходят через отличный от нуля минор Δ r -го порядка матрицы А.

Доказательство. Так как ранг матрицы А равен r, то существует по меньшей мере один минор Δ порядка r матрицы А, отличный от нуля, а миноры более высокого порядка равны нулю. В частности, миноры -го порядка, содержащие в свою очередь Δ в качестве минора, равны нулю.

Обозначим через 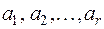, строки матрицы А, проходящие через минор А. Если бы эти строки были линейно зависимы, то одна из них линейно выражалась бы через остальные, а потому одна из строк минора А линейно выражалась бы через его остальные строки. Вычитая из этой строки минора соответствующую линейную комбинацию его остальных строк, мы эту строку превратили бы в yулевую, и получилось бы, что 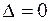, т. е. противоречие с условием 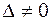. Следовательно, строки 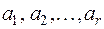матрицы А линейно независимы.

Обозначим через а какую-нибудь из остальных строк матрицы А. Тогда должен существовать такой набор чисел 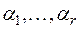из поля Р, что 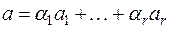, т.е. строка а линейно выражается через строки 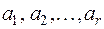матрицы А (это следует из свойства однородных систем уравнений с ).

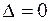Транспонируя матрицу А, мы подобным же образом докажем теорему и для столбцов ■.

Теорема 2. Ранг системы строк матрицы А равен рангу r матрицы А и тому же числу r равен ранг системы столбцов матрицы А.

Доказательство. Возьмем произвольно 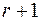строк матрицы А. Матрица A₁ размера 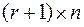, строками которой являются , будет, очевидно, иметь ранг k, не превосходящий r. Отсюда по теореме 1 в матрице A₁ должна существовать линейно независимая система k строк, а остальные строки матрицы A₁ должны линейно выражаться через эту систему строк. Следовательно, все 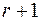строк матрицы A₁ будут линейно зависимы. Мы видим, что любая система 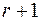строк матрицы А линейно зависима. Вместе с тем по теореме 1 должна существовать в матрице А система r линейно независимых строк. Таким образом, ранг системы строк матрицы А равен r.

Для столбцов матрицы А доказательство проводится аналогичным образом ■.

Пример. Найти линейную зависимость между векторами вещественного пространства четырехмерных строк:

, .

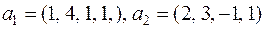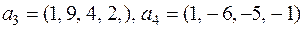Составляем матрицу, строками которой являются данные векторы:

.

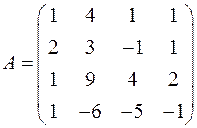Нетрудно убедиться, что ранг матрицы равен двум, причём минор второго порядка 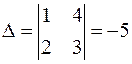отличен от нуля.

Так как элементы определителя Δ расположены в первых двух строках матрицы А, то векторы 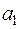и 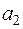линейно независимы, а векторы а₃ и а₄ через них линейно выражаются. Впрочем, здесь будет также линейно независимой и любая пара векторов, так как не равны нулю, например, и другие миноры второго порядка матрицы А.

Найдем, как выражаются векторы а₃ и а₄ через 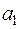и 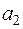. Для этой цели пишем равенство: ,

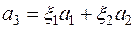или подробнее: .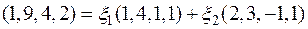

Производя в правой части равенства умножение векторов на числа и сложение векторов: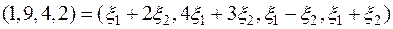

получаем такую систему уравнений:

.

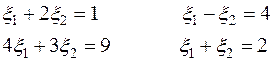Ограничимся первыми двумя уравнениями. Определителем из коэффициентов этих двух уравнений будет транспонированный определитель Δ. Поскольку 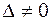, система двух уравнений с двумя неизвестными

.

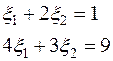должна иметь решение и при том единственное. Без труда находим, что 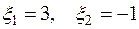Следовательно, .

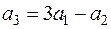Подобным же образом можно установить, что .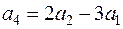

Определение: Назовем линейное пространство V над числовым полем Рn -мерным, а число п – размерностью пространства V, если в V существует по меньше мере одна линейно независимая система п векторов и всякая система из большего числа векторов уже линейно зависима. Мы будем n -мерное пространство обозначать через 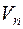и иногда будем называть его конечномерным.

Если в пространстве V можно найти линейно независимую систему, состоящую из любого числа векторов, то V называется бесконечномерным.

Пример 1. Пространство n -мерных строк над числовым полем Р является n -мерным.

В самом деле, возьмем произвольную систему s векторов этого пространства, :

,

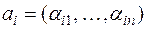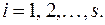
Матрица А размера , строками которой являются векторы 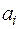, имеет, очевидно, ранг 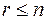. Следовательно, s строк матрицы А линейно зависимы, т. е. система векторов 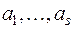линейно зависима. Легко видеть далее, что система п векторов 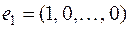, , 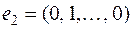…, 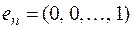уже линейно независима.

В дальнейшем пространство n -мерных строк над полем Р будет обозначаться через .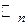

Пример 2. Пространство всех многочленов от х над числовым полем Р бесконечномерно.

В самом деле, если для некоторых чисел 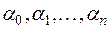из Р имеет место равенство 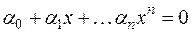, то согласно определению равенства двух многочленов получается, что 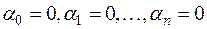, т. е, система векторов 1, х,..., х^п рассматриваемого пространства при любом п линейно независима.

Определение: Назовем базисом n -мерного пространства V _n такую конечную линейно независимую систему векторов 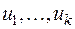, через которую линейно выражается любой вектор х пространства V _n:

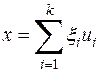
где 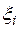— числа из поля Р. Мы будем эту систему 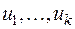рассматривать как упорядоченную, т. е. два базиса, отличающиеся лишь порядком следования векторов, будем считать различными.

Теорема 1: В п - мерном пространстве V всегда существует по меньшей мере один базис, а именно всякая линейно независимая система п векторов образует базис V _n.

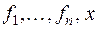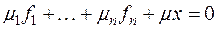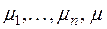Доказательство: В самом деле, пусть — какая-нибудь линейно независимая система п векторов. Присоединяя к ней произвольный вектор х,получим систему п + 1 векторов , т. е. линейно зависимую систему: , где – числа из поля Р, среди которых по меньшей мере одно отлично от нуля. Если бы число 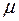. равнялось нулю, то получилось бы равенство 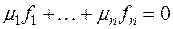с ненулевым набором чисел 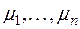что противоречит линейной независимости системы . 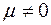Следовательно, , и вектор x: линейно выражается через систему векторов , т. е. эта система векторов образует базис пространства V _n. ■.

Нулевое пространство (т. е. линейное пространство, состоящее из одного нулевого вектора) не является n-мерным, так как в нем не существует конечной линейно независимой системы векторов. Но этому пространству мы будем приписывать размерность, равную нулю.

Теорема 2. Любой вектор n-мерного пространства V _n выражается через базис 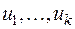единственным образом.

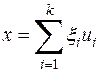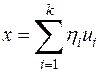Доказательство: Пусть вектор x имеет два выражения через базис: и . Вычитая почленно из первого равенства второе, получаем 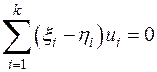. В силу линейной независимости базиса отсюда следует, что 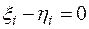или 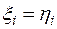, i = 1,2,..., k ■.

Коэффициенты 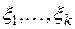линейного выражения вектора х через базис называются координатами вектора х (в данном базисе), и, таким образом, мы можем каждому вектору х пространства V _n поставить во взаимно однозначное соответствие k -мерную строку 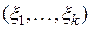или k -мерный столбец 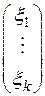его координат, так называемую координатную строку или координатный столбец.

Пользуясь правилом умножения прямоугольных матриц, можно выражение вектора х через базис 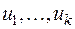записать в матричной форме, а именно в виде

,

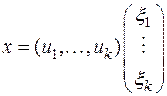здесь элементами однострочной матрицы 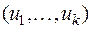являются векторы базиса.

Можно привести самые разнообразные примеры линейных пространств над данным полем Р одинаковой размерности, но все они в отношении свойств алгебраических операций ничем не будут друг от друга отличаться,. Это утверждение мы сформулируем ниже более точно, когда познакомимся с понятием изоморфизма линейных пространств.

Дата добавления: 2015-05-29