
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение линейного векторного пространства
|
|
|
|
Из курса аналитической геометрии известно, что любая точка плоскости (при заданной системе координат) определяется двумя координатами, т.е. упорядоченной парой двух вещественных чисел, аналогично и любой вектор на плоскости. Любая точка трёхмерного пространства определяется тремя координатами, а вектор, в пространстве, тремя компонентами. Однако в геометрии, механике и физике приходится изучать такие объекты, для задания которых недостаточно трёх вещественных чисел.
Рассмотрим совокупность шаров в трёхмерном пространстве. Для того, чтобы шар был полностью определён нужно задать координаты его центра и радиус, т.е. задать упорядоченный набор четырёх вещественных чисел, из которых последнее – R – может принимать только положительные значения.
Рассмотрим различные положения твёрдого тела в пространстве. Для его определения нужны: - координаты центра тяжести (3 числа); - направление некоторой фиксирующей оси, проходящей через центр тяжести (2 числа – 2 из 3-х направляющих косинусов) и угол поворота вокруг этой оси. Т.е. система из 6 вещественных чисел.
Эти примеры указывают на целесообразность рассмотрения совокупности всевозможных упорядоченных систем из n совокупностей вещественных чисел.
Введём некоторые понятия.
Упорядоченный набор n чисел  , называется n- мерным вектором; где
, называется n- мерным вектором; где 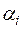 , (
, ( ) – координаты вектора
) – координаты вектора 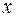 . Целесообразно дать «бескоординатное» определение векторного пространства, не требующее задания векторов упорядоченными наборами чисел. Такое определение – аксиоматическое, в нем ничего не будет сказано о свойствах отдельного вектора, но будут перечислены свойства, которыми должны обладать операции над векторами.
. Целесообразно дать «бескоординатное» определение векторного пространства, не требующее задания векторов упорядоченными наборами чисел. Такое определение – аксиоматическое, в нем ничего не будет сказано о свойствах отдельного вектора, но будут перечислены свойства, которыми должны обладать операции над векторами.
Пусть Р – некоторое числовое поле (оно, в частности, может быть полем вещественных или полем комплексных чисел) и V – некоторое множество, природа элементов которого не важна. Условимся элементы множества V обозначать малыми латинскими буквами а, b, c,..., а числа из Р – малыми греческими буквами  .
.
Пусть во множестве  определены:
определены:
1) операция сложения, ставящая каждой паре элементов а, b из V в соответствие единственный элемент a+b того же множества V, называемый их суммой;
2) операция умножения на вещественное число, ставящая в однозначное соответствие числу 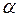 из Р иэлементу а из V элемент
из Р иэлементу а из V элемент  того же множества V.
того же множества V.
Определение: Элементы множества V будут называться векторами, а само V – вещественным линейным (или векторным) пространством, если для указанных операций (1, 2) выполняются следующие свойства, называемые аксиомами линейного пространства:
I. Свойства сложения:
1. коммутативность: а + b = b + а, где а, b произвольные элементы множества V;
2. ассоциативность  для любых элементов a, b, c рассматриваемого множества V;
для любых элементов a, b, c рассматриваемого множества V;
3. в множестве V существует по меньшей мере один такой элемент 0, называемый нулевым, что 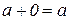 для любого а из V;
для любого а из V;
4. для всякого  данного множества существует по меньшей мере один такой элемент
данного множества существует по меньшей мере один такой элемент  , называемый противоположным элементом к а, что
, называемый противоположным элементом к а, что  .
.
II. Свойства умножения:
5. дистрибутивность относительно сложения чисел: если  – числа из P и а, b произвольные элементы V, то
– числа из P и а, b произвольные элементы V, то  ,
,
6. дистрибутивность относительно сложения векторов:  .
.
7. ассоциативность относительно умножения чисел: если  – числа из числового поля P и а – произвольный элемент рассматриваемого множества V, то
– числа из числового поля P и а – произвольный элемент рассматриваемого множества V, то 
8. для любого элемента  и для числа 1 из P справедливо равенство
и для числа 1 из P справедливо равенство  .
.
Примеры линейных пространств:
1) Множество квадратных матриц n -го порядка с элементами из поля  . комплексных чисел образуют линейное пространство над полем
. комплексных чисел образуют линейное пространство над полем  . относительно операций сложения матриц и умножения матрицы па число.
. относительно операций сложения матриц и умножения матрицы па число.
2) Множество прямоугольных матриц размера 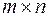 с комплексными элементами также образуют линейное пространство над полем комплексных чисел К относительно тех же операций, причем роль 0 играет здесь прямоугольная матрица, у которой все элементы равны нулю.
с комплексными элементами также образуют линейное пространство над полем комплексных чисел К относительно тех же операций, причем роль 0 играет здесь прямоугольная матрица, у которой все элементы равны нулю.
3) Множество многочленов от х степени 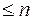 над числовым полем Р с установленными в нем обычными операциями сложения многочленов и умножения многочлена на число образует, как нетрудно проверить, линейное пространство над Р.
над числовым полем Р с установленными в нем обычными операциями сложения многочленов и умножения многочлена на число образует, как нетрудно проверить, линейное пространство над Р.
4) Точно так же образует линейное пространство над числовым полем Р множество всех (т. е. без ограничения степени) многочленов от х над Р стеми же операциями сложения многочленов и умножения многочлена на число.
5) Напротив, множество многочленов от х одной и той же степени 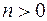 над числовым полем Р с теми же операциями, что и в предыдущем примере, не образует линейного пространства над Р, так как сумма двух многочленов степени п может оказаться многочленом меньшей степени.
над числовым полем Р с теми же операциями, что и в предыдущем примере, не образует линейного пространства над Р, так как сумма двух многочленов степени п может оказаться многочленом меньшей степени.
6) Множество вещественных функций вещественноой переменной х, непрерывных на отрезке [ а, b ], сустановленными на нем обычными операциями сложения функций и умножения функции на вещественное число образует линейное пространство над полем вещественных чисел  .
.
Множество n -мерных строк  (т. е. однострочных матриц, состоящих из n чисел) с элементами
(т. е. однострочных матриц, состоящих из n чисел) с элементами  , принадлежащими некоторому числовому полю P, образует линейное пространство над полем Р относительно операций сложения матриц и умножения матрицы на число. Это так называемое пространство п-мерных строк над полем Р. Аналогично множество n-мерных столбцов с элементами
, принадлежащими некоторому числовому полю P, образует линейное пространство над полем Р относительно операций сложения матриц и умножения матрицы на число. Это так называемое пространство п-мерных строк над полем Р. Аналогично множество n-мерных столбцов с элементами  , принадлежащими некоторому числовому полю P, образует линейное пространство над полем Р относительно тех же операций, так называемое пространство n-мерных столбцов над Р.
, принадлежащими некоторому числовому полю P, образует линейное пространство над полем Р относительно тех же операций, так называемое пространство n-мерных столбцов над Р.
7) Рассмотрим в трехмерном пространстве  множество
множество  геометрических векторов (направленных отрезков) с одним и тем же началом О (0, 0, 0). В качестве операций рассмотрим сложение векторов по правилу параллелограмма и умножение направленного отрезка на число. В число элементов рассматриваемого множества включается и точка О. Легко убедиться, что относительно этих операций трехмерное пространство векторов
геометрических векторов (направленных отрезков) с одним и тем же началом О (0, 0, 0). В качестве операций рассмотрим сложение векторов по правилу параллелограмма и умножение направленного отрезка на число. В число элементов рассматриваемого множества включается и точка О. Легко убедиться, что относительно этих операций трехмерное пространство векторов  образует линейное пространство над полем вещественных чисел.
образует линейное пространство над полем вещественных чисел.
В дальнейшем линейное пространство над полем вещественных чисел будет коротко называться вещественным линейным пространством, а линейное пространство над полем комплексных чисел – комплексным линейным пространством.
Отметим некоторые простейшие следствия, вытекающие из определения линейного пространства.
1. В сумме нескольких векторов можно слагаемые произвольным образом объединять в скобки и произвольным образом менять порядок следования слагаемых, сумма от этого не изменяется.
2. В линейном пространстве существует только один нулевой вектор.
Доказательство: Докажем «от противного». Пусть наряду с  существует
существует  , тогда
, тогда  , с другой стороны
, с другой стороны 

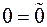 ■ (черный квадрат – квадрат Халмоша, в дальнейшем будет обозначать «что и требовалось доказать»).
■ (черный квадрат – квадрат Халмоша, в дальнейшем будет обозначать «что и требовалось доказать»).
3. Для всякого вектора а существует только один противоположный вектор – а.
Доказательство: Докажем «от противного». Пусть существует два противоположных элемента:  и
и 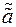 , т.е.
, т.е.  и
и  . Рассмотрим
. Рассмотрим  , с другой стороны
, с другой стороны 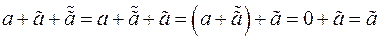 ,
,  ■.
■.
4. Из аксиом 1.-4. следует существование и единственность разности: 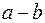 .
.
Доказательство: В линейном пространстве V уравнение 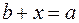 однозначно разрешимо для любых векторов а и b. Обозначим единственное решение этого уравнения через
однозначно разрешимо для любых векторов а и b. Обозначим единственное решение этого уравнения через 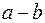 – разность векторов а и b. Действительно,
– разность векторов а и b. Действительно,  есть решение уравнения
есть решение уравнения 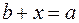 , т.к.
, т.к.  . Единственность решения: если
. Единственность решения: если 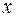 — какое-нибудь решение уравнения
— какое-нибудь решение уравнения 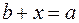 , то прибавляя к обеим частям этого равенства противоположный вектор
, то прибавляя к обеим частям этого равенства противоположный вектор  , получаем:
, получаем:  ,
,  ,
,  ,
,  ■.
■.
5. 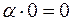 .
.
Доказательство: В самом деле, если  произвольный вектор, то
произвольный вектор, то  ■.
■.
6.  .
.
Доказательство: Если  – произвольное число из поля Р, то
– произвольное число из поля Р, то  ■.
■.
7. Если  , то или
, то или 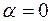 или
или 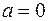 .
.
Доказательство: Если  , то существует
, то существует  :
:  , если
, если 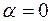 , то получим 6-е свойство ■.
, то получим 6-е свойство ■.
8.  .
.
Доказательство:  , т.е.
, т.е. 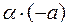 – противоположный элемент для
– противоположный элемент для 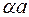 ■.
■.
9.  .
.
Доказательство:  , т.е.
, т.е.  – противоположный элемент для
– противоположный элемент для 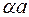 ■.
■.
10.  .
.
11.  .
.
В дальнейшем аксиомы 1.-8. и следствия 1.-11. будем использовать без оговорок.
|
|
|
|
|
Дата добавления: 2015-05-29; Просмотров: 1642; Нарушение авторских прав?; Мы поможем в написании вашей работы!